Home
School Exams
Scholarship Exams
OTI365 - NTSE - X Standard
NTSE Mental Ability Test - Analytical Reasoning Important Questions with Answer

NTSE Mental Ability Test - Analytical Reasoning

Exam Duration: 45 Mins Total Questions : 30

1 )

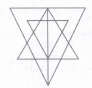
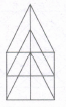
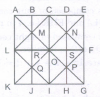
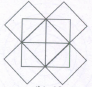
What is the number of triangles that can be formed whose vertices are the vertices of an octagon but have only one side common with that of octagon?

(a)
64
(b)
32
(c)
24
(d)
16

Solution :

When the triangles are drawn in an octagon with vertices same as those of the octagon and have one side common to that of the octagon, the figure will appear as shown in (Fig. 1).

Now, we shall first consider the triangles having only one side AB common with octagon ABCDEFGH and having vertices common with the octagon (See Fig. 2). Such triangles are ABD, ABE, ABF and ABG i.e. 4 in number.

Similarly, the triangles having only one side BC common with the octagon and also having vertices common with the octagon are BCE, BCF, BCG and BCH (as shown in Fig. 3). i.e. There are 4 such triangles. This way, we have 4 triangles for each side of the octagon. Thus, there are 8 x 4 = 32 such triangles

2 )

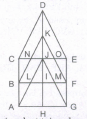
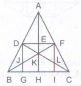
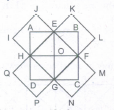
Find the number of triangles in the given figure.

(a)
27
(b)
25
(c)
23
(d)
21

Solution :

The figure may be labelled as shown

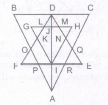
The simplest triangles are GLK, DLJ, DJM, HMN, QRE, IRA, IPA and FPO i.e. 8 in number.
The triangles having two components each are BDO, CDQ, DLM, PRA, KFI, NEI, HJI, GJI, DKI and DNI i.e. 10 in number.
The triangles having four components each are DIE, DFI, DOA, DQA and GHI i.e. 5 in number.
The triangles having six components each are DCA and DBA i.e. 2 in number.
DEF is the only triangle having eight components.
ABC is the only triangle having twelve components.
Thus, there are 8 + 10 + 5 + 2 + 1 + 1 = 27 triangles in the figure.

3 )

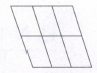
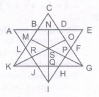
Count the number of parallelogram in the given figure.

(a)
20
(b)
18
(c)
16
(d)
12

Solution :

The figure may be labelled as shown. The simplest Parallelograms are ABFE, BCGF, CDHG, EFJI, FGKJ and GHLK. These are 6 in number.

The parallelograms composed of two components each are ACGE, BDHF, EGKI, FHLJ, ABJI, BCKJ and CDLK. Thus, there are 7 such parallelograms.
The parallelograms composed of three components each are ADHE and EHLI i.e. 2 in number.
The parallelograms composed of four components each are ACKI and BDLJ i.e. 2 in number
There is only one parallelogram composed of six components, namely ADLI
Thus, there are 6 + 7 + 2 + 2 + 1 = 18 parallelograms in the figure.

4 )

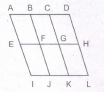
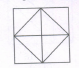
How many triangles and parallelograms are there in the following figure?

(a)
21, 17
(b)
19, 13
(c)
21, 15
(d)
19, 17

Solution :

The figure may be labelled as shown.

Triangles: The simplest triangles are KJN, KJO, CNB, OEF, JJL, JIM, BLA and MFG i.e. 8 in number.
The triangles composed oftwo components each are CDJ, EDJ, NKO, JLM, JAR and JGH i.e. 6 in number.
The triangles composed of three components each are BKI, FKI, CJA and EJG i.e. 4 in number.
The triangles composed of four components each are 7. CDE and AJG i.e. 2 in number.
The only triangle composed of six components is BKF.
Thus, there are 8 + 6 + 4 + 2 + 1 = 21 triangles in the given figure.
Parallelograms: The simplest parallelograms are NJLB and JOFM i.e. 2 in number.
The parallelogram composed of two components each are CDKB, DEFK, BIHA and IFGH i.e., 4 in number
The parallelogram composed of three components each are BKJA, KFGJ, CJIB and JEFI i.e.4 in number
There is only one parallelogram i.e. BFGA composed of four components
The parallelograms composed of five components each are CDJA, DEGJ, CJHA and JEGH i.e. 4 in number.
The only parallelogram composed of six components is CEFB.
The only parallelogram composed of ten components is CEGA.
Thus, there are 2 + 4 + 4 + 1 + 4 + 1 + 1 = 17 parallelograms in the given figure.

5 )

Count the number of pentagons in the adjoining figure.

(a)
16
(b)
12
(c)
8
(d)
4

Solution :

The figure may be labelled as shown.

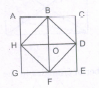
The pentagons in the figure are ABDFH, CDFHB, EFHBD, GHBDF, ACDFG, CEFHA, EGHBC, GABDE, BDEGH, DFGAB, FHACD and HBCEF. Thus, these are 12 in number.

6 )

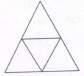
Find the number of triangles in the given figure.

(a)
4
(b)
5
(c)
6
(d)
7

Solution :

The figure may be labelled as shown

The simplest triangles are ADE, BDF, DEF and EFC
i.e. 4 in number.
There is only one triangle ABC composed of four components.
Thus, there are 4 + 1 = 5 triangles in the given figure.

7 )

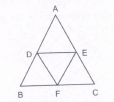
Find the number of triangles in the given figure.

(a)
16
(b)
18
(c)
19
(d)
21

Solution :

The figure may be labelled as shown.

The simplest triangles are EFH, BIC, GHJ, GIJ, EKD and CKD i.e. 6 in number
The triangles composed of two components each are ABJ, AFJ, GCK, GEK, CED arid GHI i.e, 6 in number
The triangles composed of three components each are GCD, GED, DJB and DJF i.e. 4 in number
The triangles composed of four components each are ABF and GCE i.e. 2 in number
The triangles composed of five components each are ABD and AFD i.e. 2 in number.
There is only one triangle i.e. FBD composed of six components.
Total number of triangles in the figure
= 6 + 6 + 4 + 2 + 2 + 1 = 21

8 )

Find the number of triangles in the given figure

(a)
11
(b)
13
(c)
15
(d)
17

Solution :

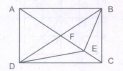
The simplest triangles are AFB, FEB, EBC, DEC, DFE and AFD i.e. 6 in number.
The triangles composed of two components each are AEB, FBC, DFC, ADE, DBE and ABD i.e. 6 in number.
The triangles composed of three components each are ADC and ABC i.e. 2 in number
There is only one triangle i.e. DBC which is composed of four components.
Thus, there are 6 + 6 + 2 + 1 = 15 triangles in the figure

9 )

Find the number of triangles in the given figure

(a)
20
(b)
24
(c)
28
(d)
32

Solution :

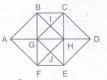
The simplest triangles are ABG, BIG, BIC, CIH, GIH, CDH, HED, GHJ, HJE, FEJ, GFJ and AGF i.e. 12 in number.
The triangles composed of two components each are ABF,CDE,GBC, BCH,GHG,BHG,GHF,GHE,HEF and GEF i.e. 10 in number.
The triangles composed of three components each are 8. ABH, AFH, CDG and GDE i.e. 4 in number.
The triangles composed of four components each are BHF and CGE i.e. 2 in number.
Total number of triangles in the figure = 12 + 10 + 4 + 2 = 28.

10 )

Find the minimum number of straight lines required to make the given figure.

(a)
11
(b)
14
(c)
16
(d)
17

Solution :

The figure may be labelled as shown.
The horizontal lines are AK, BJ, CI, DH and EG i.e. 5 in number.
The vertical lines are AE, LF and KG i.e. 3 in number.

The slanting lines are LC, CF, FI, LI, EK and AG i.e. 6 in number.
Thus, there are 5 + 3 + 6 = 14 straight lines in the figure.

11 )

What is the number of straight lines and the number of triangles in the given figure?

(a)
10 straight lines and 34 triangles
(b)
9 straight lines and 34 triangles
(c)
9 straight lines and 36 triangles
(d)
10 straight lines and 36 triangles

Solution :

The figure may be labelled as shown.

The Horizontal lines are DF and BC i.e. 2 in number.
The Vertical lines are DG, AH and FI i.e. 3 in number.
The Slanting lines are AB, AC, BF and DC i.e. 4 in number.
Thus, there are 2 + 3 + 4 = 9 straight lines in the figure.
Now, we shall count the number of triangles in the figure.
The simplest triangles are ADE, AEF, DEK, EFK, DJK, FLK, DJB, FLC, BJG and LIC i.e. 10 in number
The triangles composed of two components each are ADF,AFK,DFK,ADK,DKB,FCK,BKH,KHC,DGB and FIC i.e. 10 in number
The triangles composed of three components each are DFJ and DFL i.e. 2 in number.
The triangles composed of four components each are ABK, ACK, BFI, CDG, DFB, DFC and BKC i.e. 7 in number.
The triangles composed of six components each are ABH, ACH, ABF, ACD, BFC and CDB i.e. 6 in number. There is only one triangle i.e. ABC composed of twelve components.
There are 10 + 10 + 2 + 7 + 6+ 1 = 36 triangles in the figure.

12 )

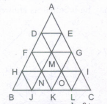
Find the number of triangles in the given figure

(a)
21
(b)
23
(c)
25
(d)
27

Solution :

The figure may be labelled as shown. The simplest triangles are ABL, BCD, DEF, FGP, PGH, QHI, JQI, KRJ and LRK i.e. 9 in number.

The triangles composed of two components each are OSG, SGQ, SPI, SRI, KSQ, KMS, FGH, JHI and JKL i.e. 9 in number.
There is only one triangle i.e. KSG which is composed of four components.
The triangles composed of five components each are NEI, ANI, MCG and KCO i.e. 4 in number
The triangles composed of six components each are GMK and KOG i.e. 2 in number.
There is only one triangle i.e. AEI composed of ten components.
There is only one triangle i.e. KCG composed of eleven components.
Therefore, total number oftriangles in the given figure
= 9 + 9 + 1 + 4 + 2 + 1 + 1 = 27

13 )

Find the number of triangles in the given figure

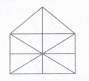
(a)
10
(b)
19
(c)
21
(d)
23

Solution :

The figure may be labelled as shown.

The simplest triangles are ABI, BIC, AIJ, CIJ, AHJ, CDJ, JHG, JDE, GJF and EJF i.e. 10 in number.
The triangles composed of two components each are ABC, BCJ, ACJ, BAJ, AJG, CJE and GJE i.e. 7 in number
The triangles composed of four components each are ACG, ACE, CGE and AGE i.e. 4 in number. Total number of triangles in the figure= 10 + 7 + 4 = 21

14 )

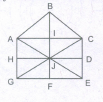
Find the minimum number of straight lines required to make the given figure

(a)
13
(b)
15
(c)
17
(d)
19

Solution :

The figure may be labelled as shown.

The horizontal lines are IJ, AB, EF, MN, HG, DC and LK i.e. 7 in number
The vertical lines are AD, EH, IL, FG, BC and JK i.e. 6 in number.
Thus, there are 7 + 6 = 13 straight lines in the figure

15 )

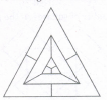
What is the minimum number of colours required to fill the spaces in the given diagram without any two adjacent spaces having the same colour?

(a)
6
(b)
5
(c)
4
(d)
3

Solution :

The figure may be labelled as shown.

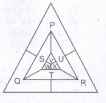
The spaces P, Q and R have to
be shaded by three different colours definitely (since each of these three spaces lies adjacent to the other two).
Now, in order that no two adjacent spaces be shaded by
the same colour, the spaces T, U and S must be shaded with the colours of the spaces P, Q and R respectively.
Also the spaces X, V and W must be shaded with the colours of the spaces S, T and V respectively i.e. with the colours ofthe spaces R, P and Q respectively. Thus, minimum three colours are required

16 )

In the adjoining figure, if the centres of all the circles are joined by horizontal and vertical lines, then find the number of squares that can be formed.

(a)
6
(b)
7
(c)
8
(d)
1

Solution :

The figure may be labelled as shown

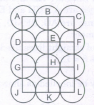
We shall join the centres of all the circles by horizontal and vertical lines and then label the resulting figure as shown.
The simplest squares are ABED, BCFE, DEHG, EFIH, GHKJ and HILK i.e. 6 in number.
The squares composed off our simple squares are ACIG and DFLJ i.e. 2 in number.
Thus, 6 + 2 = 8 squares will be formed.

17 )

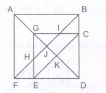
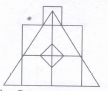
Count the number of triangles and squares in the given figure.

(a)
21 triangles, 7 squares
(b)
18 triangles, 8 squares
(c)
20 triangles, 8 squares
(d)
22 triangles, 7 squares

Solution :

The figure may be labelled as shown.

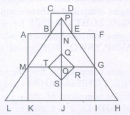
Triangles: The simplest triangles are BPN, PNE, ABM, EFG, MLK, GHI, QRO, RSO, STO and QTO i.e. 10 in number
The triangles composed of two components each are BPE, TQR, QRS, RST and STQ i.e. 5 in number.
The triangles composed of three components each are MPO and GPO i.e. 2 in number
The triangles composed of six components each are LPJ, HPJ and MPG i.e. 3 in number
There is only one triangle LPH composed of twelve components.
Total number of triangles in the figure
= 10 + 5 - 2 + 3 + 1 = 21
Squares: The squares composed of two components each are KJOM and JIGQ i.e ..2 in number.
The squares composed of three components each are ANOM, NFGO and CDEB i.e.3 in number.
There is only one square i.e. QRST composed of four components
There is only one square i.e. AFIK composed of ten components.
Total number of squares in the figure
=2+3+1+1=7

18 )

Count the number of squares in the given figure.

(a)
11
(b)
21
(c)
24
(d)
26

Solution :

The figure may be labelled as shown.

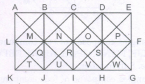
The squares composed of two components each are BNQM, CORN, DPSO, MQTL, NRUQ, OSVR, PFWS, QUJT, RVIU and SWHV i.e. 10 in number
The squares composed of four components each are ABQL, BCRQ, CDSR, DEFS, LQJK, QRIJ, RSHI and SFGH i.e. 8 in number.
The squares composed of eight components each are BRJL, CSIQ and DFHR i.e. 3 in number
The squares composed of sixteen components each are ACIK, BDHJ and CEGI i.e. 3 in number
Thus, there are 10 + 8 + 3 + 3 = 24 squares in the figure.

19 )

Count the number of squares in the given figure.

(a)
22
(b)
20
(c)
18
(d)
14

Solution :

The figure may be labelled as shown

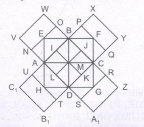
The squares composed of two components each are BJMI, CKMJ, DLMK and AIML i.e. 4 in number.
The squares composed of three components each are EBMA, BFCM, MCGD and AMDH i.e. 4 in number.
The squares composed of four components each are VWBA, XYCB, ZA₁DC.and B₁C₁AD i.e. 4 in number.
The squares composed of seven components each are NOJL, PQIU, RSLJ and TUIK i.e. 4 in number.
There is only one square i.e. ABCD composed of eight components
There is only one square i.e. EFGH composed of twelve components.
Total number of squares in the figure
= 4 + 4 + 4 + 4 + 1 + 1 = 18

20 )

Count the number of rectangles in the given figure

(a)
20
(b)
18
(c)
16
(d)
15

Solution :

The figure may be labelled as shown.

The rectangles composed of two components each are HUE, EKJF, FMNG, GPQH, AEOH, EBFO, OFCG and HOGD i.e. 8 in number.
The rectangles composed of four components each are ABFH, BCGE, CDHF, DAEG and EFGH i.e. 5 in number
The rectangles composed of six components each are IJFG, KLGH, MNHE and PQEF i.e. 4 in number
The rectangles composed of eight components each are IJMN, KLPQ and ABCD i.e. 3 in number.
Thus, there are 8 + 5 + 4 + 3 = 20 rectangles' in the given figure

21 )

Count the number of parallelograms in the given figure

(a)
47
(b)
45
(c)
41
(d)
39

Solution :

The figure may be labelled as shown.

The parallelograms composed of two components each are ADME, DFNM, EMOG, FHJN, MNKO, GOLI, HBJN, NJKO, OKLI, FHNM, MNOG, DFME, HJKN, NKLO, OLCI, FNOM, MOIG and DMGE. i.e. 18 in number.
The parallelograms composed of four components each are HOKB, NILJ, FGOH, HOLJ, NICK, FGIN, FMJB, DENH, MGKJ, MGCL, DEIO, FMLK, AENF, AGOD, DMJH, DOKF, EILM and EGKN i.e. 18 in number
The parallelograms composed of six components each are AEJH, DAIL, DECL, DEJB, HILB and HICJ i.e. 6 in number.
The parallelograms composed of eight components each are FGKB, FGCK and AGKF i.e. 3 in number. Total number of parallelograms in the figure
=18 + 18 + 6 + 3 = 45

22 )

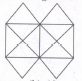
What is the minimum number of straight lines that is needed to construct the figure?

(a)
11
(b)
13
(c)
15
(d)
21

Solution :

The figure may be labelled as shown.

The horizontal lines are AE and JF i.e. 2 in number.
The vertical lines are AJ, CH and EF i.e. 3 in number.
The slanting lines are AG, BF, JD, IE, AB, DE, JI and FG i.e. 8 in number.
Total number of straight lines needed to construct the figure = 2 + 3 + 8 = 13

23 )

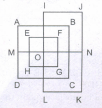
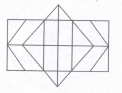
Determine the number of rectangles and hexagons in the given figure

(a)
30, 5
(b)
32, 3
(c)
28, 5
(d)
30, 3

Solution :

The figure may be labelled as shown.

Rectangles: The simplest rectangles are CVSR, VETS, RSWM and STKW i.e. 4 in number.
The rectangles composed of two components each are CETR, VEKW, RTKM and GVWM i.e. 4 in number.
The rectangles composed of three components each are AQRP, PRMO, EGHT and THIK i.e. 4 in number.
The rectangles composed of four components each are GEKM, AVSP,TSWO, VGHS and SHIW i.e. 5 in number.
The rectangles composed of five components each are AETP, PTKO,CGHR and RHIM i.e. 4 in number.
The rectangles composed of six components each are ACMO and EGIK i.e. 2 in number.
The rectangles composed of eight components each are AGHP, PHIO, AVWO and vcrw i.e. 4 in number.
The rectangles composed of ten components each are AEKO and CGIM i.e. 2 in number.
AGIO is the only rectangle having sixteen components. Total number of rectangles in the given figure
= 4 + 4 + 4 + 5 + 4 + 2 + 4 + 2 + 1 = 30.
Hexagons: The hexagons in the given figure are CDEKLM, CEUKMQ, CFHJMQ, BEUKNP and BFHJNP.
So, there are 5 hexagons in the given figure

24 )

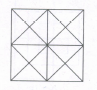
Count the number oftriangles and squares in the given figure.

(a)
44 triangles, 10 squares
(b)
14 triangles, 16 squares
(c)
27 triangles, 6 squares
(d)
36 triangles, 9 squares

Solution :

The figure may be labelled as shown.

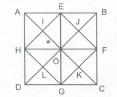
Triangles: The simplest triangles are AEI, EOI, OHI, HAl, EBJ, BFJ, FOJ, OEJ, HOL, OGL, GDL, DHL, OFK, FCK, CGK and GOK i.e. 16 in number.
The triangles composed of two components each are RAE, AEO, EOH, OHA, OEB, EBF, BFO, FOE, DHO, HOG, OGD, GDH, GOF, OFC, FCG and CGO i.e. 16 in number.
The triangles composed of foarcomponents each are HEF, EFG, FGH, GHE, ABO, BGO, CDO and DAO i.e. 8 in number
The triangles composed of eight components each are DAB, ABC, BCD and CDA i.e. 4 in number
Total number of triangles in the figure
= 16 + 16 + 8 + 4 = 44
Squares: The squares composed oftwo components are HIOL, IEJO, JFKO and KGLO i.e. 4 in number.
The squares composed of four components are AEOH, EBFO, OFGC and HOGD i.e.4 in number.
There is only one square EFGH which is composed of eight components.
There is only one square ABCD which is composed of sixteen components.
Total number of squares in the figure
= 4 + 4 + 1 + 1 = 10

25 )

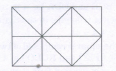
Count the number of squares in the given figure

(a)
6
(b)
7
(c)
9
(d)
10

Solution :

The figure may be labelled as shown

The squares composed of two components each are ABKJ, BCLK, CDEL, LEFG, KLGH and JKHI i.e. 6 in number.
There is only one square i.e. CEGK composed of four components
The squares composed of eight components each are ACGI and BDFH i.e. 2 in number.
There are 6 + 1 + 2 = 9 squares in the figure

26 )

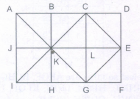
Count the number of squares in the given figure.

(a)
13
(b)
16
(c)
19
(d)
20

Solution :

The figure may be labelled as shown

The simplest squares are BCNM, CDON, PQIJ and QRHI i.e. 4 in number
The squares composed of two components each are MNTS, NOUT, STQP and TURQ i.e. 4 in number
The squares composed of five components each are ACTL, CEFT, TFGI and LTIK i.e. 4 in number
The squares composed of six components each are BDUS and SUHJ i.e. 2 in number.
There is only one square i.e. MORP composed of eight components
There is only one square i.e. AEGK composed of twenty components
Total number of squares in the figure
= 4 + 4 + 4 + 2+1 + 1 = 16

27 )

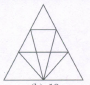
Find the number of triangles in the given figure.

(a)
12
(b)
18
(c)
22
(d)
26

Solution :

The figure may be labelled as shown.

The simplest triangles are AHB, GHI, BJC, GFE, GIE, IJE, CEJ and CDE i.e. 8 in number
The triangles composed of two components each are HEG, BEC, HBE, JGE and ICE i.e. 5 in number.
The triangles composed of three components each are FHE, GCE and BED i.e. 3 in number.
There is only one triangle i.e. AGC composed of four components.
There is only one triangle i.e. AFD composed of nine components.
Thus, there are 8 + 5 + 3 + 1 + 1 = 18 triangles in the given figure.

28 )

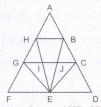
Count the number of rectangles in the given figure

(a)
8
(b)
17
(c)
18
(d)
20

Solution :

The figure may be labelled as shown

The simplest rectangles are ABQP, PQNO, BCDN, NDEM, MEFL, LFJK, FGHR and RHIJ i.e. 8 in number.
The rectangles composed of two components each are ABNO, BCEM, NDFL, MEJK and FGIJ i.e. 5 in number.
The rectangles composed of three components each are ACDO, BCFL, NDJK and LGIK i.e..4 in number. There is only one rectangle i.e. BCJK composed of four components.
Total number of rectangles in the figure = 8 +5 +4 + 1 = 18

29 )

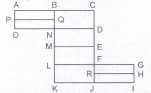
Count the number of squares in the given figure

(a)
32
(b)
30
(c)
29
(d)
28

Solution :

The figure may be labelled as shown

The simplest squares are ABGF, BCHG, CDIH, DEJI, FGLK, GHML, HINM, IJON, KLQP, LMRQ, MNSR, NOTS, PQVU, QRWV, RSXW and STYX i.e. 16 in number.
The squares composed of four components each are ACMK, BDNL, CEOM, FHRP, GISQ, HJTR, KMWU, LNXV and MOYWi.e. 9 in number.
The squares composed of nine components each are ADSP, BETQ, FIXU and GJYV i.e. 4 in number. There is one square AEYU· composed of sixteen
components
There are 16 +9 +4 +1 = 30 squares in the given figure

30 )

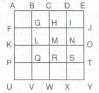
Count the number of triangles and squares in the given figure.

(a)
26 triangles, 5 squares
(b)
28 triangles, 5 squares
(c)
26 triangles, 6 squares
(d)
28 triangles, 6 squares

Solution :

The figure may be labelled as shown.

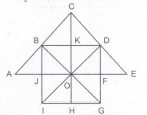
Triangles: The simplest triangles are JBO, BKO,KDO, DFO, FGO, GHO, HIO, IJO, ABJ, BCK, CKD and DEF i.e.12 in number.
The triangles composed of two components each are lBO, BDO, DGO, GIO, ABO, CDO, CBO, CBDand DEO i.e. 9 in number.
The triangles composed of four components each are lBD, BDG, DGI, GlB, ACO and COE i.e. 6 in number. There is only one triangle i.e. ACE composed of eight components.
Thus, there are 12 + 9 + 6 + 1 = 28 triangles in the given figure
Squares: The squares composed of two components each are BKOJ, KDFO, OFGH and JOHI i.e. 4 in number
There is only one square i.e. CDOB composed of four components.
There is only one square i.e. BDGI composed of eight components
Thus, there are 4 + 1 + 1 = 6 squares in the given figure