Home
School Exams
Scholarship Exams
OTI365 - NTSE - X Standard
NTSE SAT Mathematics - Circles Important Questions with Answer

NTSE SAT Mathematics - Circles

Exam Duration: 45 Mins Total Questions : 30

1 )

The distance between two points A and B is 3 em. A circle of radius 1.7 cm is drawn to pass through those points. Find the distance of AB from the centre of the circle

(a)
0.64
(b)
\(\sqrt { 0.64 } \)
(c)
0.8cm
(d)
0.08 cm

Solution :

Let a be the centre of the circle of radius 1.7 cm, which is drawn to pass through A and B. From a draw OD^{\(\bot \)}AB. The OD is the required distance

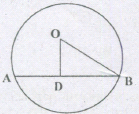
AD=DB= 1.5 cm (perpendicular from centre bisects chord)
.'. In right angled \(\Delta l\quad \Delta \)ODB
OD² = OB²- DB²(By Pythagoras theorem)
= (1.7)²- (1.5)²
= 0.64
OD =\(\sqrt { 0.64 } \) = 0.8cm

2 )

A circular dice of radius 6 em is divided into three sectors with central angles 90°, 120° and 150°. What part of the whole circle is the sector with central angle 150"? Calculate the ratio of the areas of the three sectors.

(a)
2:3:4
(b)
4:5:6
(c)
1:2:3
(d)
3:4:5

Solution :

\(\frac { Area\quad of\quad the\quad Sector\quad with\quad 0=150^{ o } }{ Area\quad of\quad the\quad circle } \)

\(=\frac { \pi \times ({ 6) }^{ 2 }\times \frac { 150 }{ 360 } }{ \pi \times ({ 6) }^{ 2 } } =\frac { 150 }{ 360 } =\frac { 5 }{ 2 } \)
Required ratio =\(\left( 36\pi \times \frac { 90 }{ 360 } \right) \)
\(=\left( 36\pi \times \frac { 120 }{ 360 } \right) =\left( 36\pi \times \frac { 150 }{ 360 } \right) \)
\(=\frac { 1 }{ 4 } :\frac { 1 }{ 3 } :\frac { 5 }{ 12 } =3:4:5\)

3 )

The distance between the centre of the two circles with radii 4 cm and 9 cm is 13 cm. The length of the direct common tangent (between two points of contact) is

(a)
13 cm
(b)
\(\sqrt { 153 } cm\)
(c)
12 cm
(d)
18 cm

Solution :

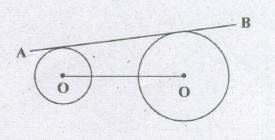
Required distance = \(\sqrt { ({ r }_{ 1 }+{ r }_{ 2 })^{ 2 }-({ r }_{ 1 }-{ r }_{ 2 })^{ 2 } } \)
=\(\sqrt { { 4r }_{ 1 }{ r }_{ 2 } } =\sqrt { 4\times 9\times 4 } \)
= 2 x 3 x 2 = 12 cm

4 )

AB is a diameter of a circle with centre at O. DC is a chord of it such that DC II AB. If = 20^o, then is equal to

(a)
120^o
(b)
110^o
(c)
115^o
(d)
100^o

Solution :

⁼ = 20^o(on same arc BC)
= 90^o(angle of semi-circle)
= 90^o + 20^o= 110^o

5 )

Two chords AB and CD of circle whose circle is 0, meet at the point P and = 50^o, = 40^o.Then the value of is

(a)
60^o
(b)
40^o
(c)
45^o
(d)
75^o

Solution :

+ =²+²
(Exterior angles of a triangle)

=
=
=^{\(\frac { 1 }{ 2 } \left( 50^{ o }+{ 40 }^{ o } \right) =45^{ o }\)}

6 )

One chord of a circle is known to be lO.lcm. The radius of this circle must be

(a)
5 cm
(b)
Greater than 5 cm
(c)
greater than or equal to 5 cm
(d)
Less than 5 cm

Solution :

The largest chord of a circle is its diameter.

7 )

If a chord of a circle of radius 5 cm is a tangent to a circle of radius 3 ern, both circles being concentric, then the length of the chord is

(a)
10 cm
(b)
12.5 cm
(c)
8 cm
(d)
7 cm

Solution :

\(AC=\sqrt { { AO }^{ 2 }-OC^{ 2 } } \)
\(\quad \quad =\quad \sqrt { { 5 }^{ 2 }-{ 3 }^{ 2 } } =\sqrt { 16 } =4\quad cm\)
AB=2x4=8cm

8 )

ABC and DBC are two right triangles with common hypotenuse BC and' with their sides AC and DB intersecting at P. then product of AP.PC is equal to product of

(a)
BD.AB
(b)
PD.AP
(c)
PC.BP
(d)
BP.PD

Solution :

=(each = one right angle)
:. Points B, A, D, Care concyclic
(angles on the same side of segment BC are equal)
AP.PC ==BP.PD (products of segments of intersecting chords of a circle)

9 )

ABC is an isosceles triangle in which AB=AC. A circle through B touching AC at its middle point D intersects AB is P, then AP=?

(a)
\(\frac { 1 }{ 4 } \quad AD\)
(b)
\(\frac { 1 }{ 4 } \quad Ac\)
(c)
\(\frac { 1 }{ 4 } \quad DC\quad \quad \)
(d)
\(\frac { 1 }{ 4 } \quad AB\)

Solution :

.'. AB is a secant and AD is a tangent to the circle
:. AB.AP=AD^{2

But AD = \(\frac { 1 }{ 2 } AC\quad \) (Given)

=^{\(\frac { 1 }{ 2 } AB\)} (:. AB = AC, given)}
:. AB.AP=\(\left( \frac { 1 }{ 2 } AB \right) ^{ 2 }=\frac { 1 }{ 4 } \quad AB^{ 2 }\)
AP =\(\frac { 1 }{ 4 } \quad AB\)

10 )

In the below figure, 0 is the centre, if r=7 cm, Ox=5 cm, find (i) Ax.xD=?, (ii) OP=17 cm, OC=8cm, PD=5 cm. Find DC=? (iii) AB=9 cm, BP=3 cm, find PT?

(a)
24 cm², 40 cm, 6 cm
(b)
40 cm², 2 cm, 12 cm
(c)
20 cm², 10 cm, 2 cm
(d)
none of these

Solution :

(i) Ax.xD==r²-Ox²=7²-5² =49-25 =24 cm²
(ii) PD.PC==OP²-r²=OP²-OC²
Let DC =x cm. Then
PD.PC=17²-8²
5(5+x) = 289-64=225
=>25+5x =225 => 5x=200 => x=40 cm
Hence DC =40 cm
(iii) PT²=PA.PB orPT==6 cm. i.e., (PT²=12 x 3=36)

11 )

In the given figure, the angle A of the triangle ABC is a right angle. The circle on AC as diameter cuts BC at D. If BD=9, DC=7, calculate the length of AB.

(a)
14
(b)
13
(c)
11
(d)
12

Solution :

Since OA is a radius, = 90^o, BA is the tangent to the circle, by the tangent radius property
Hence, BA²=BDxBC ==9x 16==144
=> BA =12

12 )

In the given figure, =42^o. Find and

(a)
128^o
(b)
138^o
(c)
118^o
(d)
none of these

Solution :

= =42^o
(angles in alternate segment) .
Now, in cyclic quadrilateral AECB
+ = 180^o
(opposite angle of a cyclic quadrilateral are supplementary)
+ 42^o= 180^o
= 138^o

13 )

A circle is inscribed in quadrilateral ABCD.If BC=38 cm BQ=27 cm, DC=25 cm and AD^{\(\bot \)}BC. Find the radius of the circle

(a)
7 cm
(b)
15 cm
(c)
14 cm
(d)
none of these

Solution :

Let the sides AD, AB. BC and CD touch the circle at point P, Q. R, S respectively.
Since, tangent to a circle is perpendicular to the radius through the point of contact.
:. OP^{\(\bot \)}AD and OS^{\(\bot \)}DC. Also AD^{\(\bot \)}DC (given)
.'. OPDS is a square
BR=BQ=27cm (tangents from an external point to a circle are equal in length)
CR=HC-BR=(38-27)cm = 11 cm
Similarly, CS=CR=1 cm
DS=DC-CS=(25-11) cm =14 cm
Radius of circle = OP =OS = 14 cm
(.'. OPDS is a square)

14 )

Two circles of radii 25 cm and 9 cm touch each other externally. Find the length of the direct common tangent?

(a)
15 cm
(b)
20 cm
(c)
25 cm
(d)
30 cm

Solution :

Let the two circles with centres A, B and q radii 25 cm and 9 cm touch each other external at point C.
Then, AB = AC+CB = (25+9) cm = 34 cm
'Let PQ be the direct common tangent
:. BQ^{\(\bot \)}PQ and AP^{\(\bot \)}PQ
Draw BR^{\(\bot \)}AP.Then BRPQis a rectangle(Tangent perpendicular radius at the point of contact)
In ^{\(\Delta \)}ABR, AB²=AR²+BR²(Pythagoras theorem)
~ (34)²=(16)²+BR²
BR=\(\sqrt { 900 } \)cm=30 cm
:. PQ=BR=30 em

15 )

If a straight line touches a circle and from the point of contact, a chord is drawn, the angles between the tangent and the chord are respectively ___________ to the angles in the alternate segments.

(a)
Parallel
(b)
Perpendicular
(c)
equal
(d)
none of these

Solution :

i) \(\lfloor a\)+ \(\lfloor x\)= 90^o(angle between tangent and radius through point of contact)
= 90^o
(Angle in a semi circle)
or \(\lfloor y\)+\(\lfloor b\)= 90^o
\(\lfloor a\)+ \(\lfloor x\)= \(\lfloor y\)+\(\lfloor b\)
But\(\lfloor x\) =\(\lfloor y\)
(angles in the same segment PSTR)
\(\lfloor a\)=\(\lfloor b\)
i.e =_{^{\(\longrightarrow \)}}1
ii) += 180^o(opposite angles of a cyclic quadrilateral PQRS)
+ = 180^o
(Adjacent angles on a straight lines)
⁺⁼⁺
Also = (from 1)
⁼ are equal

16 )

How many tangents can be drawn to a circle at any project of it?

(a)
1
(b)
2
(c)
3
(d)
none of these

17 )

How many parallel tangents can a circle have at the most?

(a)
1
(b)
2
(c)
3
(d)
none of these

18 )

Two circles of radii 5 cm and 3 cm touch each other internally, the distance between their centres is

(a)
5 cm
(b)
3 cm
(c)
2 cm
(d)
8 cm

Solution :

Distance = 5 cm - 3 cm = 2 cm

19 )

From a point Q, the length of the tangent to a circle is 24cm and the distance of Q from the centre is 25cm. The radius of the circle is

(a)
7 cm
(b)
5 cm
(c)
12 cm
(d)
1 cm

Solution :

OP²+PQ²=OQ² (By Pythagoras theorem)

^{\(\Rightarrow \)}OP²+24²=25²
^{\(\Rightarrow \)}OP =7 cm

20 )

If TPand TQare the two tangents to a circle with centre O so that =100^o, then is equal to

(a)
60^o
(b)
80^o
(c)
50^o
(d)
120^o

Solution :

+= 180^o
\(\Rightarrow \)+100^o= 180^o
= 80^o

21 )

In the given figure, PA and PB are tangents such that PA=9cm and =60^o. Find the length of chord AB

(a)
9 cm
(b)
6 cm
(c)
7 cm
(d)
4 cm

Solution :

Since, the lengths of tangents drawn from a point to a circle are equal, we have
PA=PB ^{\(\Rightarrow \)} = x^o(say)
Then,x+x+60^o=180^o
2x+60^o=180^o
2x=120^o
x=60^o
Thus, each angle of ^{\(\Delta \)}PAB=60°
:. A PABis an equilateral triangle:
:.AB=PB=PA=9cm

22 )

Two tangents segments BC and BD are drawn to a circle with centre O such that = 120^o, then OB =

(a)
BC
(b)
thrice of BC
(c)
twice of BC
(d)
none of these

Solution :

Join OB, OC and OD
= 60^o and = 90^o
= 30^o
\(\frac { BC }{ OB } \)= Sin 30^o=\(\frac { 1 }{ 2 } \Rightarrow \)OB= 2 BC

23 )

Inthe given figure, 0 is the centre of two concentric circles of radii 4 cm and 6 cm respectively. PA and PB are tangents to the outer and inner circle respectively. If PA=10cm, find the length of PB up to one place of decimal.

(a)
\(\sqrt { 120\quad cm } \)
(b)
\(\sqrt { 110 } cm\)
(c)
\(\sqrt { 130 } cm\)
(d)
none of these

Solution :

Join, OA, OB and OP. Then OB=4cm, OA=6cm and PA=10cm
OP²=OA²+PA²=6²cm²+(10)²cm²=136 cm²
BP =\(\sqrt { { OP }^{ 2 }-{ OB }^{ 2 } } =\sqrt { 136-16 } =\sqrt { 120\quad}cm\)

24 )

The ratio of the area of a circle and an equilateral triangle whose diameter and side are equal, is

(a)
\(\sqrt { 3 } :\pi \)
(b)
\(\pi :\sqrt { 2 } \)
(c)
\(\pi :\sqrt { 3 } \)
(d)
\(\pi :1\)

Solution :

\(\frac { Area\quad of\quad circle\quad }{ Area\quad of\quad equilateral\quad triangle } \)
\(=\frac { \pi \left( \frac { r }{ 2 } \right) ^{ 2 } }{ \frac { \sqrt { 3 } }{ 4 } { r }^{ 2 } } =\frac { \frac { { \pi r }^{ 2 } }{ 4 } }{ \sqrt { 3 } \frac { { r }^{ 2 } }{ 4 } } =\pi :\sqrt { 3 } \)

25 )

A square is circumscribing a circle. The side of the square is 14cm. Find the area of the square not included in the circle

(a)
21 cm²
(b)
42 cm²
(c)
48 cm²
(d)
196 cm²

Solution :

Required area = Area of square - Area of circle
= 14x 14-\(\pi \left( \frac { 14 }{ 2 } \right) ^{ 2 }\)= 196 -154 = 42 cm²

26 )

What is the supplementary angle of the central angle of a semicircle?

(a)
0^o
(b)
90^o
(c)
180^o
(d)
360^o

Solution :

Central angle of a semi-circle =\(\frac { { 360 }^{ o } }{ 2 } \)=180^o
.'. Its supplementary angle = 180°-180°=0°

27 )

In the following figure, CP and CQ are two tangents lines of a circle with centre O. ARB is another tangent line of the circle which touches the circle at the point R. If CP= 11 cm and BC= 7 em, Find length of BR.

(a)
1 cm
(b)
2 cm
(c)
3 cm
(d)
4 cm

Solution :

BR = RQ = CQ - CB
= CP - CB = 11-7 == 4 cm

28 )

In the adjoining figure, ^{\(\Delta \)}ABC, Circumscribes a circle. Find the length of BC.

(a)
6 cm
(b)
8 cm
(c)
10 cm
(d)
12 cm

Solution :

BC = BP + PC = BR + CQ
=3 +(AC-AQ)
=3 +AC-AR
=3+11-4 = 10 cm

29 )

In the given figure, find the length of the chord AB if PA=6cm and = 60^o

(a)
2 cm
(b)
4 cm
(c)
6 cm
(d)
5 cm

Solution :

PA =PB =6 cm
\(\lfloor A\)=60^o;\(\lfloor B\)=60^o
\(\lfloor P\)= 60^o(Angle sum property of a _{^{\(\Delta \)}}le)
:. \(\Delta \)APBis equilateral :. AB=PA=PB=6cm

30 )

The length of the minute hand of a clock is 14 em. Find the area swept by the minute hand in 5 minutes.

(a)
\(\frac { 134 }{ 2 } cm^{ 2 }\)
(b)
\(\frac { 154 }{ 3 } cm^{ 2 }\)
(c)
\(\frac { 144 }{ 3 } cm^{ 2 }\)
(d)
none of these

Solution :

r = 14 cm
\(\theta =\frac { 90^{ o } }{ 3 } =30^{ o }\)
:. Area swept = \(\frac { \theta }{ { 360 }^{ o } } \times \pi r^{ 2 }\)
=\(\frac { 30^{ o } }{ { 360 }^{ o } } \times \frac { 22 }{ 7 } \times 14\times 14\)
=\(\frac { 154 }{ 3 } cm^{ 2 }\)