Home
School Exams
Scholarship Exams
OTI365 - NTSE - X Standard
NTSE SAT Mathematics - Linear Equation in Two Variables Important Questions with Answer

NTSE SAT Mathematics - Linear Equation in Two Variables

Exam Duration: 45 Mins Total Questions : 25

1 )

A number consists of two digits such that the digit in the ten's place is less by 2 than the digit in the units place.Three times the number added to \(6\over 7\) times the numberobtained by reversing the digits equals 108. The sum of the digits in the number is

(a)
6
(b)
7
(c)
8
(d)
9

Solution :

Let the unit's digit be x
Then, ten's digit = (x - 2)
∴ 3[10(x -2) +x ]+\({6\over 7}\)[x +(x -2)] = 108
231x - 420 + 66x -12 = 756
⇒ 297x = 1188 ⇒ X = 4
Hence, sum of the digits = x + (x - 2)
= 2x - 2
=6

2 )

A two digit number is such that the product of the digit is 8. When 18 is added to the number, then the digits are reversed. The number is

(a)
18
(b)
24
(c)
42
(d)
81

Solution :

Let the ten's and unit's digit be x and \(8\over x\) respectively
Then,\(\left(10x+{8\over x} \right)+18=10\times{8\over x}+x\)
⇒ 10x² + 8 + 18x = 80 + x²
⇒ 9x² + 18x - 72 = 0 ⇒ x²+2x - 8 = 0
⇒ (x+4)(x-2)=0
⇒ x=2
So, ten's digit = 2 and
Unit's digit = 4. Hence, required number = 24

3 )

Eighteen years ago, a father was three times as old as his son.Now the father is only twice as old as his son. Then the sum of the present ages of the son and the father is

(a)
54
(b)
72
(c)
105
(d)
108

Solution :

Let the present ages of the father and son be 2x and x respectively
Then, (2x - 18)=3(x - 18)
⇒ x = 36
∴ Requlredsum=( 2x + x) = 3x = 108years

4 )

A person's present age is two fifth of the age of his mother.After 8 years, he will be one-half of the age of his mother.How old is the mother at present?

(a)
32 year
(b)
36 years
(c)
40 years
(d)
48 years

Solution :

Let the mother's present age be x years
Then, the person's present age \(=\left({2\over 5}x \right)\) years
\(∴\left({2\over 5}x+8 \right)={1\over 2}(x+8)\)
⇒ 2( 2x + 40) = 5( x + 8) ⇒ x = 40

5 )

A and B each has some money. If A gives Rs. 30 to B then B will have twice the money left with A. But, if B gives Rs.10 to Athen A will have thrice as much as is left with B. How much money does each have?

(a)
62, 34
(b)
60, 34
(c)
62, 30
(d)
none of these

Solution :

Suppose A and B have Rs.x and Rs.y respectively.
Case I
When A gives Rs. 30 to B
Money with A = Rs.(x - 30), with B = Rs.(y + 30)
(y+30) = 2(x-30) = 2x-y = 90
Case II
When B gives Rs.10 to A
Money with A = Rs.(x + 10), with B = ~ (y-10)
(x+10) = 3 (y-10)=x-3y=-40 Rs.(2)
Solving (1) and (2) y = 34, x = 62
Hence, A has Rs.62, B = Rs.34

6 )

If three times the larger of two numbers is divided by the smaller one, we get 4 as the quotient and 3 as the remainder Also, if seven times the smaller number is divided by the larger one, we get 5 as the quotient and t as the remainder.Find the numbers.

(a)
20, 18
(b)
25,17
(c)
25, 18
(d)
none of these

Solution :

Let the larger number be x and smaller number be y
We know,
Dividend = (divisor x quotient) x remainder
We have,
3x = 4Y + 3 ⇒ 3x - 4Y = 3 ⟶ (1)
7x = 5Y +1 ⇒ 5x - 7Y = -1 ⟶ (2)
Multiply (1) by 5, (2) by 3 and subtract. we get y = 18
Substitute y = 18 in (1) we get
3x - (4 x 18 ) '= 3 ⇒ 3x = 75 ⇒ x = 25
Hence, the required numbers are 25, 18

7 )

If \({1\over2(2x+3y)}+{12\over7(3x-2y)}={1\over2}{7\over (2x+3y)}+{4\over 3x-2y}=2\) then the value of (2x + 3y) is

(a)
7
(b)
6
(c)
\(1\over 7\)
(d)
none of these

Solution :

Take \({1\over (2x+3y)}=u\)and \({1\over (3x-2y)}=v\)
Then, \({u\over 2}+{12v\over 7}={1\over 2}⇒7u+24v=7⟶(1)\)
7u+4v=2⟶(2)
Subtract (2) from (1) we get
20v = 5 ⇒ \(1\over 4\)
Substitute \(v={1\over 4}\)in (2) we get
\(7u+\left( 4\times{1\over 4}\right)=2⇒7u+1=2\)
\(⇒u={1\over 7}\)
Now, \(u={1\over 7}⇒{1\over (2x+3y)}={1\over 7}⇒(2x+3y)=7\)
\(v={1\over 4}⇒(3x-2y)=4\)

8 )

Rs. 1 and Rs. 5 coins are available (as many requireD).
Find the smallest payment which cannot be made by these coins, if not more than 5 coins are allowed.

(a)
3
(b)
14
(c)
12
(d)
18

Solution :

14 is the required number, because
14 = 5+5+1+1+1+1
Here, for the payment of~ 14 six coins are required.
So, we cannot make payment of Rs.14, by given coins

9 )

Suppose you walk from home to the bus stand at 4 km/hour and immediately return at x km/hour. If the average speed is 6 km/hour, then the value of x is

(a)
8 km/hr
(b)
10 krn/hr
(c)
12 krn /hr
(d)
none

Solution :

Let the distance from home to bus stand = 5km
\(6={25\over {5\over 4}+{5\over x}}\)
\(3={4x\over x+4}\)
⇒ 3x+12 = 4x
x = 12 km/hr

10 )

7 pens and 3 books cost Rs. 1395, while 5 pens and 4 books cost Rs. 1665, find the cost of a pen and that of a book

(a)
55, 360
(b)
45,360
(c)
35,350
(d)
none of these

Solution :

Let the cost of each pen be Rs.x and
each book be Rs.y
7x+3y=1395 ⟶ (1)
5x+4y = 1665 ⟶ (2)
Multiply(1) by 4 and (2) by 3 we get
13x = 585 ⇒ X = 45
Substitute x = 45 in (1) we get
(7X45)+3y = 1395
⇒ 3y= 1395- 315 = 1080 ⇒ Y = 360
∴ cost of 1 pen = Rs.45 and
costof 1 book = Rs.360

11 )

The sum of the digits of a two digit number is 12. The number obtained by inter-changing its digits exceeds the given number by 18. Find the number.

(a)
75
(b)
77
(c)
55
(d)
57

Solution :

Let the tens digit of the required number be x and the units digit be y. Then
x + y = 12 ⟶ (1)
Required number = (10x + y)
Number obtained on reversing
the digits = (10y + x)
∴ (10y + x) - (10x + y) =1'8 ⇒ 9y - 9x =18
⇒ y - x = 2 ⟶ (2)
On adding (1) and (2) we get
2y=14 ⇒ y=7
Substitute y = 7 in (1) we get
X + 7 = 12 ⇒ X = (12 -7) = 5
X =5,y =7
Hence, the required number is 57.

12 )

Arvind has Piggy bank. It is full of one-rupee and fifty paise coins. It contains 3 times as many fifty-paise coins as one rupee coins. The total amount of the money in the bank is Rs. 35.How many coins of each kind are there in the bank?

(a)
14, 42
(b)
15, 42
(c)
14, 52
(d)
none of these

Solution :

Letx be one rupee coins in the bank
Number of 50-paise coins = 3x
∴ Valueof x one rupee coins = Rs.x
Valueof 3x fifty-paise coins = 50 x 3x paise
= 150x paise
\(=Rs{150\over 100}x=Rs{3x\over 2}\)
∴ Totalvalue of all coins =\(Rs.\left(x+{3x\over2} \right)\)
But, the total amount of money in bank is given = Rs.35
\(∴\ x+{3x\over 2}=35\)
5x = 70 ⇒ x = 14
∴ No. of one rupee coins = 14,
No.of 50-paise coins = 3x = 3 x 14 = 42

13 )

Hamid has three boxes of different fruits. Box A weighs \(2{1\over 2}\) kg more than Box B and Box C weighs \(10{1\over 4}\)kg more than Box B.The total weight of the boxes is \(48{3\over 4}\) How many kgs does Box A weights?

(a)
\(15{1\over 2}kg\)
(b)
\(14{1\over 2}kg\)
(c)
\(13{1\over 2}kg\)
(d)
none of these

Solution :

Let Box B weights = x kg
Since, Box A weight \(2{1\over 2}\)kg more than Box B and
Box C weights\(10{1\over 4}\) kg more than Box B.
Weight of Box \(A=\left( x+2{1\over 2}\right)kg=x+{5\over2 }kg⟶(1)\)
Weight of Box \(C=\left( x+10{1\over 4}\right)kg=x+{41\over4 }kg\)
Total weight of all boxes \(=\left( x+{5\over2}+x+x+{41\over 4}\right)kg\)
But, total weight of boxes is \(48{3\over 4}kg={195\over 4}kg\)
\(x+{5\over 2}+x+x+{41\over 4}={195\over 4}\)
⇒ 4x + 10 + 4x + 4x+41= 195
12x + 51=195
12x = 144
x = 12
Substitute x = 12 in (1)
Weight of Box \(A=\left( 12+{5\over 2}\right)kg=14{1\over 2}kg\)

14 )

The sum of the numerator and the denominator of a fraction is 12. If the denominator is increased by 3, the fraction becomes \(1\over 2\).Find the fraction.

(a)
\(3\over 7\)
(b)
\(2\over 7\)
(c)
\(4\over 7\)
(d)
\(5\over 7\)

Solution :

Lethe required fraction be \(x\over y\) . Then
x +y = 12 ⟶ (1) and
\({{x\over y+3}}={1\over 2} ⇒ 2x = Y + 3 ⇒ 2x - y = 3 ⟶ (2)\)
Add (1) and (2) we get
3x = 15 ⇒ x = 5
Substitutex = 5 in (l) we get
5+y=12 ⇒ y=12-5=7
x = 5,Y= 7. Hence, the required fraction \(={5\over 7}\)

15 )

The sum of two numbers is 1000 and the difference between their squares is 256000. Find the numbers.

(a)
638 and 372
(b)
538 and 362
(c)
628 and 372
(d)
none of these

Solution :

Let the larger number be x
and the smaller number be y
Then, x + y = 1000 ⟶ (1)
X² - y² = 256000 ⟶ (2)
On dividing (2) by (1) we get
\({x^2-y^2\over x+y}={256000\over 1000}⇒x-y=256⟶(3)\)
Add (1) and (3), we get, 2x = 1256 ⇒ x = 628
Substitute x = 628 in (1) we get y = 372
Hence, the required numbers are 628 and 372

16 )

Five years ago, A was thrice as old as B and ten years later A shall be twice as old as B. What are the present ages of A and B?

(a)
30,40
(b)
20, 50
(c)
30, 50
(d)
none of these

Solution :

Let the present ages of B and A be x years and y
years respectively. Then
B's age 5 years ago = (x - 5) years
A's age 5 years ago = (y - 5) years
∴ 1(y - 5) = 3(x - 5) ⇒ 3x - Y = 10 ~ (1)
B's age 10 years hence = (x+10) years
A's age 10 years hence = (y+ 10) years
∴ (y +10) = 2(x+l0) ⇒ 2x - Y = -10 ⟶ (2)
On subtracting (2) from (1), we get x = 20
Substituting x = 20 in (1) we get
(3 X 20) - y = 10 ⇒ Y= 50
∴ x = 20, Y= 50
Hence, B's present age = 20 years
A's present age = 50 years

17 )

A takes 3 hours more than B to walk 30 km. But, if A doubles his pace, he is ahead of B by \(1{1\over2}\)hours. Find their speeds of walking?

(a)
\(3{1\over 3}\) km/hr, 5km/hr
(b)
\(2{1\over 3}\) km/hr, 5km/hr
(c)
\(1{1\over 3}\) km/hr, 5km/hr
(d)
none of these

Solution :

Let A's speed = x krn/hour and
B's speed = y km/hour
Then, the time taken by A to cover 30km =\({30\over x}hrs\)
And, the time taken by B to cover 30km=\({30\over y}hrs\)
\(∴\ {30\over x}-{30\over y}=3⇒{1\over x}-{1\over y}={1\over 10}⟶ (1)\)
Again, A's speed = 2x km/hr and
B's speed = y krn/hr
Then, time taken by A to cover 30 km \(={30\over 2x}hrs\)
time taken by B to cover 30 km = \({30\over y}hrs\)
\(∴\ {30\over y}-{30\over 2x}={3\over 2}⇒{2\over y}-{1\over x}={1\over 10}⟶(2)\)
Substitute y = 5 in (1).
we get\({1\over x}=\left({1\over 10}+{1\over 5} \right)={3\over 10}⇒x={10}\)
∴ A's speed\(={10\over 3}\)krn/hr =\(3{1\over 3}\)km/hr and
B's speed = 5km/hr

18 )

90% and 97% pure acid solutions are mixed to obtain 21litres of 95% pure acid solution. Find the quantity of each type of acid to be mixed to form the mixture.

(a)
5, 15
(b)
6, 14
(c)
5, 15
(d)
none of these

Solution :

Let the given solution -be labelled as A and B respectively
Let x litres of A be mixed with y litres of B
Then x+ y =21 ⟶ (1)
Quantity of acid in x litres of A = (90% of x) litres
\(=\left(x\times{90\over 100} \right)\) litres =\({9x\over 10}\)litres
Quantity of acid in y litres of B = (97% of y) litres
\(=\left(y\times{90\over 100} \right)\)litres =\({9y\over 10}\)litres
Quantity of acid in 21 litres of (A+ B)
= 95% of 21 litres=\(\left(21\times{95\over 100} \right)\)litres \({399\over 20}\)litres
\({9x\over 10}+{97y\over 100}={399\over 20}⇒90x+97y=1995⟶(2)\)
Multiplying (1) by 90 and subtracting the result from (2)
Weget 7y=105 ⇒ y=15
Substitute y = 15 in (1). we get x+ 15 = 21
⇒ x=6
∴ x=6,y=15
So, 6 litres of 90% solution is mixed with 15 litres of 97% solution.

19 )

A fraction becomes \({2\over 3}\)when 1 is added to both its numerator and denominator. And, it becomes \(1\over 2\)when 1 is subtracted from both the numerator and denominator. Find the fraction

(a)
\(2\over 5\)
(b)
\(3\over 5\)
(c)
\(1\over 5\)
(d)
none of these

Solution :

Let the required fraction be \(x\over y\).Then,
\({x+1\over y+1}={2\over 3}⇒3x-2y = -1 ⟶ (1)\)
\({x-1\over y-1}={2\over 3}⇒2x-y = -1 ⟶ (2)\)
Solve (1) and (2) we get x = 3, Y = 5
∴ Required fraction =\(3\over5\)

20 )

If the sum of a number and its square is 182. What is the number?

(a)
15
(b)
26
(c)
28
(d)
none of thesse

Solution :

Let the number be x.
Then
x + x²= 182 ⇒ x²+ x - 182 =0
⇒ (x+14)(x-13) =0
⇒ x=13

21 )

For what value ofk, the system of equations 2x + ky = 1, 3x - 5y = 7, has no solutions?

(a)
\(k={-10\over 3}\)
(b)
\(k={10\over 3}\)
(c)
\(k={3\over 10}\)
(d)
none of these

Solution :

\({2\over 3}={k\over -5}\neq{1\over 7}⇒k={-10\over 3}\)

22 )

Find the value of a so that the point (3, a) lies on the line represented by 2x - 3y = 5

(a)
1
(b)
3
(c)
1/3
(d)
-1/3

Solution :

2(3) -3a = 5
-3a = 5-6
-3a =-1
\(a={1\over 3}\)

23 )

What is the condition that the lines ax + by = c and lx + my = n are coincident?

(a)
\({a\over l}={b\over m}={c\over n}\)
(b)
\({a\over l}={b\over m}\neq{c\over n}\)
(c)
\({a\over l}\neq{b\over m}\)
(d)
\({b\over m}\neq{a\over l}\)

24 )

Determine the value of c for which the system of linear equations ex + 3y = 3, 12x + cy = 6 has no solution?

(a)
6
(b)
-6
(c)
±6
(d)
3

Solution :

\({c\over 12}={3\over c}\neq{3\over 6}⇒c=-6\)

25 )

A man has only 20-p and 25-p coins in his bag.If he has 100 coins in all, totalling Rs.22.00, how many coins of each kind does be have?

(a)
60, 40
(b)
65, 35
(c)
75, 25
(d)
none of these

Solution :

Let the number of 20-p and 25-p coins be x and y respectively. Then,
x + y = 100 ⟶ (1) and
\({x\over 5}+{y\over 4}=22⇒4x+5y=440⟶(2)\)

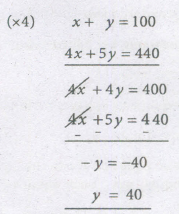
Substitute y = 40 in x + y = 100
x + 40 = 100
x = 60
x = 60, y = 40