Home
School Exams
Scholarship Exams
OTI365 - NTSE - X Standard
NTSE SAT Mathematics - Probability Sample Questions with Answer

NTSE SAT Mathematics - Probability

Exam Duration: 45 Mins Total Questions : 30

1 )

In a simultaneous throw of a pair of dice, find the probability of getting a total more than 7?

(a)
\(\frac{4}{5}\)
(b)
\(\frac{1}{12}\)
(c)
\(\frac{5}{12}\)
(d)
none of these

Solution :

Here n{S)={6x 6)=36
Let E=Event of getting a total more than 7
= {{2,6) (3,5) (3,6) (4,4) (4,5) (4,6) (5,3) (5,4) (5,5) (5,6) (6,2) (6,3) (6,4) (6,5) (6,6)}
\(\therefore P(E)=\frac{n(E)}{n(S)}=\frac{15}{36}=\frac{5}{12}\)

2 )

A bag contains 6 white and 4 black balls. Two balls are drawn at random. Find the probability that they are of the same colour.

(a)
\(\frac{7}{15}\)
(b)
\(\frac{6}{15}\)
(c)
\(\frac{4}{15}\)
(d)
none of these

Solution :

Let S be the sample space. Then, n{S)=Number of ways of drawing 2' balls out of (6+4) = 10 C₂ =\(\frac{10\times9}{2\times1}=45\)
Let E= "Event of getting both balls of same colour. Then, n{E)= number of ways of drawing (2 balls out of 6) or (2 balls out of 4)
\(=(6C_2+4C_2)=\frac{(6\times5)}{(2\times1)}+\frac{(4\times3)}{(2\times1)}=15+6=21\)
\(\therefore P(E)=\frac{n(E)}{n(S)}=\frac{21}{45}=\frac{7}{15}\)

3 )

A die is in the shape of a tetrahedron as shown, on each face, one of the numbers 1, 2, 3 or 4"is written. This die is tossed. Find the probability of getting a-prime number.

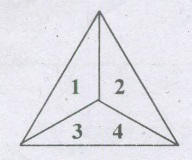
(a)
\(\frac{1}{2}\)
(b)
\(\frac{1}{3}\)
(c)
1
(d)
0

Solution :

Number of all possible outcomes (L, 2, 3, 4) = 4
Number of favourable outcomes (2, 3) = 2

4 )

In class X, there are 18 girls and 12 boys. The names of all the girls and boys are written on a card and are placed in a box. These cards are mixed up thoroughly and a card is drawn at random. What is the probability that the name card, will be that of a girl student?

(a)
\(\frac{1}{5}\)
(b)
\(\frac{2}{5}\)
(c)
\(\frac{3}{5}\)
(d)
\(\frac{4}{5}\)

Solution :

Number of favourable outcomes = 18 as there are 18 girls in class X
Number of all possible outcomes (l8 girls + 12 boys) = 30
\(\frac{18}{30}=\frac{3}{5}\)

5 )

From a pack of 52 cards, one card is drawn at random. What is the probability that the card drawn is a ten or a spade?

(a)
\(\frac{4}{13}\)
(b)
\(\frac{1}{4}\)
(c)
\(\frac{1}{13}\)
(d)
\(\frac{1}{26}\)

Solution :

n{S)=52
There are 13 spades (including one ten) and there are 3 more tens
Let E=event of getting a ten or a spade
Then, n{E)= (l3+3)=16
\(\therefore P(E)=\frac{n(E)}{n(S)}=\frac{16}{52}=\frac{4}{13}\)

6 )

Tickets numbered 1 to 20 are mixed up and then a ticket is drawn at random. What is the probability that the ticket drawn bears a number which is a multiple of 3?

(a)
\(\frac{3}{10}\)
(b)
\(\frac{3}{20}\)
(c)
\(\frac{2}{5}\)
(d)
\(\frac{1}{2}\)

Solution :

S={l, 2, 3, 4, .....19, 20}
Let E= event of getting of multiple of 3 = {3, 6, 9, 12, 15, 18}
\(\therefore P(E)=\frac{n(E)}{n(S)}=\frac{3}{10}\)

7 )

Anunbiaseddice is rolled twice, what; is the probability of not getting a 2 in anyone of the two rolls?

(a)
\(\frac{5}{2}\)
(b)
\(\frac{25}{36}\)
(c)
\(\frac{1}{3}\)
(d)
\(\frac{35}{36}\)

Solution :

P(getting a 2)= \(\frac{1}{6}\)
So, P(not getting a 2) =1-\(\frac{1}{6}=\frac{5}{6}\)
P(not getting a 2 in 2 rolls of an unbiased dice)
\(=\frac{5}{6}\times\frac{5}{6}=\frac{25}{36}\)

8 )

A coin is tossed 5 times. What is the probability of getting number of heads, more than the number of tails?

(a)
\(\frac{1}{3}\)
(b)
\(\frac{1}{32}\)
(c)
\(\frac{5}{32}\)
(d)
\(\frac{1}{2}\)

Solution :

In 5 tossed a coin, number of heads > of tails
10 Cases 5 Cases 1Case
(H H H T T) (H H H H T) (H H H H H)
Thus P(heads > tails)
=\(10\times(\frac{1}{5})^{5}+5(\frac{1}{2})^{5}+(\frac{1}{2})^{5}\)
=\(\frac{1}{32}(10+5+1)=\frac{1}{2}\)

9 )

When two dice are rolled together, the probability of getting an even number on one dice and a multiple of 3 on the other is

(a)
\(\frac{1}{6}\)
(b)
\(\frac{7}{36}\)
(c)
\(\frac{4}{9}\)
(d)
\(\frac{5}{36}\)

Solution :

Total number of outcomes =36 favorable outcomes
={(2,2) (3,2) (2,6) (6,2) (4,3) (3,4) (6,6)}
Thus, P(even number on one and multiple of 3 on another) =\(\frac{7}{36}\)

10 )

In a class of 80 students, 48 are boys and the rest of the students are girls. If 10 students shift to the other class room and a student is selected at random from the remaining class, what is the probability that a girl is selected?

(a)
\(\frac{11}{35}\)
(b)
\(\frac{27}{70}\)
(c)
\(\frac{11}{40}\)
(d)
can't be determined

Solution :

We do not know the number of girls in class after 10 students shifted, probability of selecting a girl from the remaining class can't be calculated.

11 )

A dice is thrown 65 times and 4 appeared 21 times. Now, in a random throw of a dice, what is the probability of getting 4?

(a)
\(\frac{1}{65}\)
(b)
\(\frac{11}{65}\)
(c)
\(\frac{21}{65}\)
(d)
none of these

Solution :

Total number of trials = 65
Number of times 4 appeared = 21
Probability of getting a 4=\(\frac{21}{65}\)

12 )

In a box, these are 8 red, 7 blue and 6 green balls. One ball is picked up randomly. What is the probability that it is neither red nor green?

(a)
\(\frac{2}{3}\)
(b)
\(\frac{3}{4}\)
(c)
\(\frac{7}{19}\)
(d)
\(\frac{8}{21}\)

Solution :

Total number of balls = (8+7+6)=21
Let E = event that the ball drawn is neither red
nor green
= event that the ball drawn is red
∴ n(E)=8
∴ \(P(E)=\frac{8}{21}\)

13 )

Which of the following is true?

(a)
0\(\le P(E)\le1\)
(b)
P(E)>1
(c)
P(E)<0
(d)
\(\frac{-1}{2}\le P(E) \le \frac{1}{2}\)

Solution :

Minimum value of number of favourable outcomes = 0
Maximum value of number of favourable outcomes Number of all possible outcomes

14 )

If the probability of the non-happening of an event is q, then the probability of happening of that event is

(a)
1-q
(b)
q
(c)
\(\frac{q}{2}\)
(d)
2q

Solution :

p(E) + \(P (\overset{-}{E})\) = 1 = 1-q

15 )

The sum of the probabilities of all the elementary events of an experiment is

(a)
1
(b)
2
(c)
2
(d)
3

Solution :

Sum of the number of favourable outcomes to all the elementary events of an experiment Number of all possible outcomes

16 )

What is the probability of getting a tail on throwing an unbiased coin ?

(a)
1
(b)
0
(c)
\(\frac{1}{2}\)
(d)
\(\frac{1}{4}\)

Solution :

Number of favourable outcomes (Tail) = 1
Number of all possible outcomes (Head, Tail=2)
Ans = \(\frac{1}{2}\)

17 )

How many faces does a die have?

(a)
2
(b)
3
(c)
6
(d)
4

Solution :

A die has six faces as it is cuboidal in shape

18 )

How many cards are of red coleur in a deck of playing cards?

(a)
13
(b)
26
(c)
39
(d)
52

Solution :

Number of cards of red colour in a deck of playing cards = 13(Diamond) + 13(Heart) = 26

19 )

How many face cards are there in a deck of playing cards?

(a)
4
(b)
3
(c)
12
(d)
13

Solution :

Number of face cards in a deck of playing cards 4(Jacks) +4(Queens) +4(Kings)= 12

20 )

The number of non-face cards in a deck of playing cards is

(a)
10
(b)
20
(c)
30
(d)
40

Solution :

Number of non-face cards = 52-12 =40
(Note: The face cards include, Jacks, Queens and Kings only)

21 )

A letter is chosen from the word CONGRATULATIONS. What is the probability that it is a vowel?

(a)
\(\frac{2}{5}\)
(b)
\(\frac{1}{2}\)
(c)
\(\frac{1}{4}\)
(d)
\(\frac{1}{5}\)

Solution :

Number of favourable outcomes (0, A, U, A, I, 0) = 6
Number of all possible outcomes 15, as there are 15 letters in the word.
Ans = \(\frac{6}{15}=\frac{2}{5}\)

22 )

Cards each marked with one of the numbers 4, 5, 6 .... 20. are placed in a box and mixed thoroughly. One card is drawn at random from the box, what is the probability of getting an even number?

(a)
0
(b)
1
(c)
-1
(d)
\(\frac{1}{2}\)

Solution :

Number of favourable outcomes = 0 as the only even prime number is 2 which is not include in the given numbers.

23 )

A number x is chosen at random from -4, -3, -2, -1,0, 1, 2, 3, 4. Find the probability that (x) ≤ 4

(a)
0
(b)
1
(c)
\(\frac{1}{2}\)
(d)
\(\frac{1}{9}\)

Solution :

Number of favourable outcomes
(-4, -3, -2, -1, 0, 1, 2, 3, 4) = 9
Number of all possible outcomes
(-4, -3, -2, -1,0, 1, 2, 3, 4) = 9

24 )

A digit is randomly taken from a logarithmic table. Find the probability that the digit is 0 or 9

(a)
\(\frac{2}{5}\)
(b)
\(\frac{1}{5}\)
(c)
\(\frac{3}{5}\)
(d)
\(\frac{4}{5}\)

Solution :

Number of favourable outcomes (0, 9) = 2 Number of all possible outcomes
(0, 1, 2, 3, 4, 5, 6, 7, 8, 9) = 10 \(\frac{2}{10}=\frac{1}{5}\)

25 )

The probability, it will rain tomorrow is 0.3. what is the probability that it will not rain tomorrow?

(a)
0.3
(b)
0.2
(c)
0.7
(d)
0.07

Solution :

\(P(E)+P(\overset{-}{E})=1\)
\(P(\overset{-}{E})=1-P(E)=1-0.3=0.7\)

26 )

Priya and Mani are friends. What is the probability that both will have the same birthday (ignoring leap year)

(a)
\(\frac{1}{365}\)
(b)
\(\frac{1}{366}\)
(c)
\(\frac{365}{366}\)
(d)
none of these

Solution :

Number of favourable outcomes = 1
Number of all possible outcomes = 365

27 )

What is the probability that the first snowfall in Srinagar next winter will take place on Sunday?

(a)
\(\frac{1}{7}\)
(b)
\(\frac{2}{7}\)
(c)
\(\frac{3}{7}\)
(d)
\(\frac{6}{7}\)

Solution :

There are 7 days in a week
Number of favourable outcomes (Sunday) = 1
Number of all possible outcomes (S, M, T, W. TH. F, S) = 7

28 )

A child has a block in the shape of a cube with one letter written on each face as follows

The cube is thrown once. What is the probability of getting A?

(a)
\(\frac{1}{3}\)
(b)
\(\frac{1}{6}\)
(c)
\(\frac{3}{7}\)
(d)
\(\frac{6}{7}\)

Solution :

Number of favourable outcomes = 2 as these are two A's
Number of all' possible outcomes = 6 \(\frac{2}{6}=\frac{1}{3}\)

29 )

A bag contains 4 red, 5 black and 3 yellow balls. Aball is taken out of the bag at random. Find the probability that the ball taken out is not of red colour,