1 )

When the price of a product was decreased by 10%, the number sold increased by 30% what was the effect on total revenue?

(a)
15%
(b)
16%
(c)
17%
(d)
none of these

Solution :

Let the price of the product be Rs.100 and
Let original sale be 100 pieces.
Total Revenue=Rs.(100\(\times \)100) =Rs.10000
New Revenue=Rs.(90\(\times\)130)=Rs.11700
\(\therefore\) Increase in revenue= \(\left( \frac { 1700 }{ 10000 } \times 100 \right) \)%=17%

2 )

In the new budget, the price of kerosene oil rose by 25%.By how much percent must a person reduce his consumption so that his expenditure on it does not increase

(a)
10%
(b)
15%
(c)
20%
(d)
none of these

Solution :

Reduce in consumption=\(\left[ \frac { R }{ 100+R } \times 100 \right] \)%
=\(\left( \frac { 25 }{ 125 } \times 100 \right) \)%=20%

3 )

If one root of the two quadratic equations x²+ax+b=0 and x²+bx+a=0 is common, then

(a)
a + b = 1
(b)
a + b = -1
(c)
ab = 1
(d)
ab = -1

Solution :

a²+ a\(\alpha\) b = 0 ........(1)
a² + b\(\alpha\) +a = 0 ......(2)
Subtracting both the equations, we get
(a-b)a+(b-a) = 0
\(\Rightarrow\) \(\alpha\) = 1
Substitute \(\alpha\)=1 in (1) to get a+b = -1

4 )

The value of a machine depreciates at the rate of 10% per annum.If its present value is Rs.1,62,000, what will be its worth after 2 years? What was the value of the machine 2 years ago?

(a)
121220,200000
(b)
131220,200000
(c)
151220,20000
(d)
none of these

Solution :

Value of the machine after 2 years
= Rs.\(\left[ 162000\times { \left( 1-\frac { 10 }{ 100 } \right) }^{ 2 } \right] \)
=Rs.\((162000\times\frac{9}{10}\times\frac{9}{10})\)=Rs.131220
Value of the machine 2 years ago
=Rs.\(\left[ \frac { 162000 }{ { \left( 1-\frac { 10 }{ 100 } \right) }^{ 2 } } \right] \)
=Rs.\(\left( 162000\times \frac { 10 }{ 9 } \times \frac { 10 }{ 9 } \right) \)=Rs.200000

5 )

In a daily form, 40 cows eat 40 bags of husk in 40 days. In how many days one cow will eat one bag of husk?

(a)
1
(b)
\(\frac { 1 }{ 40 } \)
(c)
40
(d)
80

Solution :

Let the required number of days be x
Less cows, more days (Indirect proportion)
.Less bags, less days (Direct Proportion)
Cows 1:40
Bags 40:1} :: 40 : x
\(\therefore 1\times 40\times x=40\times 1\times 40\Rightarrow x=40\)

6 )

If the n^th term of a progression has a linear expression in n, this progression is an AP if every terms of the given progression differs from its preceding term by

(a)
1
(b)
constant
(c)
can't be determined
(d)
none of these

Solution :

T_n=a_n+b, where a and b are constants
Then, T_n-1=a(n-1)+b,
T_n-2=a(n-2)+b,
T_n-3=a(n-3)+b, etc.,
∴ (T_n-T_n-1)=(a_n+b)-[a(n-1)+b]
=a which is independent of n
Similarly (T_n-1- T_n-2)=a
(T_n-2-T_n-3)= a and soon.

7 )

ABCD is a cyclic trapezium whose sides AD and BC are parallel to each other. If=72^\(\circ\) then the measure of the is

(a)
162^\(\circ\)
(b)
18^\(\circ\)
(c)
108^\(\circ\)
(d)
72^\(\circ\)

Solution :

=180^\(\circ\)
\(\Rightarrow\)=180^\(\circ\)-72^\(\circ\)=108^\(\circ\)
AD||BC
=72^\(\circ\)

8 )

The roots of the quadratic equation (x-12) (2x+25)=0 are

(a)
\(-12,\frac { -25 }{ 2 } \)
(b)
\(12,\frac { -25 }{ 2 } \)
(c)
\(-12,\frac { 25 }{ 2 } \)
(d)
\(12,\frac { 25 }{ 2 } \)

Solution :

x - 12 = 0 \(\Rightarrow\) x = 12,
2x + 25 = 0
x =\(-\frac { 25 }{ 2 } \)

9 )

The number of coins of radius 0.75 cm and thickness 0.2 cm to be melted to make a right circular cylinder of height 8 em and base radius 3 cm is

(a)
460
(b)
500
(c)
600
(d)
640

Solution :

Volume of one coin =\(\left( \frac { 22 }{ 7 } \times \frac { 75 }{ 100 } \times \frac { 75 }{ 100 } \times \frac { 2 }{ 10 } \right) cm\)
=\(\frac { 99 }{ 280 } { cm }^{ 3 }\)
Volume of larger cylinder=\(\left( \frac { 22 }{ 7 } \times 3\times 3\times 8 \right) { cm }^{ 3 }\)
∴Number of Coins =\(\left( \frac { 22\times 9\times 8 }{ 7 } \times \frac { 280 }{ 99 } \right) =640\)

10 )

The slant height of a conical mountain is 2.5 km and the area of its base is 1.54 krn², The height of the mountain is

(a)
2.2 km
(b)
2.4 km
(c)
3 km
(d)
3.11 km

Solution :

Let the radius of the base be r km. Then
\({ \pi r }^{ 2 }=1.54\Rightarrow \left( \frac { 1.54\times 7 }{ 22 } \right) =0.49\)
⇒ r=0.7km
Now, I = 2.5km,r = 0.7km
\(\therefore \quad h=\sqrt { { (2.5) }^{ 2 }-{ (0.7) }^{ 2 } } km\)
\(=\sqrt { 5.76 } km=2.4km\)
So, height of the mountain = 2.4 km

11 )

How many terms of AP 3, 5, 7, 9 ..... must be added to get the sum 120?

(a)
20
(b)
15
(c)
10
(d)
none of these

Solution :

a = 3, d = 2
Let the required number of terms be n. Then,
\(S_n=120 \Rightarrow \frac{n}{2} [2a+(n-1)d]=120\)
\(\Rightarrow \frac{n}{2}[2\times3 +(n-1)2]=120\)
\(\Rightarrow \frac{n}{2}(2n+4)=120\)
\(\Rightarrow = n(n+2)=120 \Rightarrow n^{2}+2n-120=0\)
=\(n^{2}+12n-10n-120=0\)
=(n+12)(n-10)=0
⇒ n=-12, n=10

12 )

If the sum of first n, 2n, 3n terms of an AP be S₁ , S₂ and S₃respectively, then

(a)
S₂=2(S₂-S₁)
(b)
S₃=3(S₂-S₁)
(c)
S₄=S₃(S₃-S₁)
(d)
none of these

Solution :

a = first term; d = common difference of the given AP.Then,
S₁ = Sum of first n terms of the given AP
S₂ = Sum of first 2n terms of the given AP
S₃ = Sum of first 3n terms of the given AP
\(\therefore S_1=\frac{n}{2}[2a+(n-1)d]\)
\(S_2=\frac{2n}{2}[2a+(2n-1)d]\)
\(S_3=\frac{3n}{2}[2a+(3n-1)d]\)
\(\Rightarrow 3(S_2-S_1)=3[2na+n(2n-1)d]-[na+\frac{1}{2}n(n-1)d]\)
\(=3.[na+\frac{3}{2}n^{2}d-\frac{1}{2}nd]\)
\(=\frac{3n}{2}[2a+3nd-d]\)
\(=\frac{3n}{2}[2a+3(n-1)d]=S,\)
Hence, S₃=3(S₂-S₁)

13 )

How many natural numbers between 1 and 1000 are divisible by 5?

(a)
197
(b)
198
(c)
199
(d)
200

Solution :

Required numbers are 5, 10, 15,20 ..... 995
Let their numbers be n. Then,
S+(n -1) x 5 = 995
⇒5(n -1) = 990
⇒n -1 = 198 => n = 199

14 )

How many terms are there in the AP 7,10,13, .... 15?

(a)
50
(b)
55
(c)
45
(d)
49

Solution :

Here a=7, d=(10-7)=3 and T_n= 151
a+(n-1)d = 151 ⇒7+(n-1) x 3 = 151
⇒3(n-1)=144 ⇒ (n-1)=48⇒n=49

15 )

The 4th term of an AP is 14 and its 12th term is 70. What is the first term?

(a)
-10
(b)
-7
(c)
7
(d)
10

Solution :

Leta be the first term and d be the common difference of the given AP.Then,
T₄= 14⇒a+3d= 14 ➝ (1)
T₁₂ = 70⇒a+11d=70 ➝(2)
On solving(1) and ➝(2)
a+3d = 14
a+11d=70
________
-8d=-56
d=7
a+3d=14 ➝(1)
Substitute d=7 in ➝(1)
a+3 x 7=14
a+21=14
a=14-21
a=-7

16 )

The first term of an AP is 6 and its common difference is 5. What will be its 11th term?

(a)
56
(b)
41
(c)
46
(d)
none of these

Solution :

Here a = 6, d = 5
T₁₁= a+10d = 6+10 x 5=56

17 )

A and B can do a work in 8 days? B and C can do the same work in 12 days. A, B and C together can finish the work in 6 days. A and C together will do in

(a)
4 days
(b)
6 days
(c)
8 days
(d)
12 days

Solution :

(A+B+C)'s 1 day's work =\(\frac { 1 }{ 6 } \)
(A+B)'s 1 day's work =\(\frac { 1 }{ 8 } \)
(B+C)'s 1 day's work =\(\frac { 1 }{ 12 } \)
\(\therefore\)(A+C)'s 1 day's work\(=\left( 2\times \frac { 1 }{ 6 } \right) -\left( \frac { 1 }{ 8 } +\frac { 1 }{ 12 } \right) \)
\(=\left( \frac { 1 }{ 3 } -\frac { 5 }{ 24 } \right) =\frac { 3 }{ 24 } =\frac { 1 }{ 8 } \)
So, A and C together will do the work in.8 days.

18 )

Prakash purchased a machine for Rs.80,000 and spent Rs.5000 on repair, Rs.1000 on transport and sold it with 25% profit. At what price did he sell the machine?

(a)
Rs.1,06,250
(b)
Rs.1,07,500
(c)
Rs.1,17,500
(d)
none of these

Solution :

C.P. =Rs.(80000+5000+1000) =Rs.86000
Profit = 25%
\(\therefore\)S.P = 125% of Rs.86000
=Rs.\(\left( \frac { 125 }{ 100 } \times 86000 \right) \)
=Rs.107500

19 )

The frequency of the class preceding the modal class in the following frequency distribution is

Marks	Number of Students
20-30	4
30-40	28
40-50	42
50-60	20
60-70	6

(a)
28
(b)
32
(c)
20
(d)
100

Solution :

The class preceding the modal class (40-50) is 30-40.

20 )

Find the sum of first 25 terms of an AP whose nth term is given by T_n=(7 - 3n)

(a)
-700
(b)
-800
(c)
+600
(d)
none of these

Solution :

T_n = (7-3n)
T₁ = 7-3 x 1=4
T₂ = 7-3x2=1
∴ a=4 and d = ( T₂ - T₁) = (1-4) = -3
∴ Sum of first 25 terms is given by
\(S_25=\frac{n}{2}[2a+(n-1)d]\) where n=25
=\(\frac{25}{2}[2\times4+(25-1)\times(-3)]\)
=\([\frac{25}{2}\times(-64)]=[25\times(-32)]=-800\)
Hence. the sum of first 25 terms is -800

21 )

If a metallic cuboids weighs 16 kg, how much would a miniature cuboid of metal weigh, if all dimension are reduced to one fourth of the origin

(a)
0.25 kg
(b)
0.50 kg
(c)
0.75 kg
(d)
1 kg

Solution :

Let the dimensions of the bigger cuboid = xyz Volume of the miniature cuboid
=\(\left( \frac { 1 }{ 4 } x \right) \left( \frac { 1 }{ 4 } y \right) \left( \frac { 1 }{ 4 } z \right) =\frac { 1 }{ 64 } xyz\)
∴ Weight of the miniature cuboid
\(=\left( \frac { 1 }{ 64 } \times 16 \right) kg=0.25kg\)

22 )

In the given figure, AB II CDand EF II GH. The values of x, y, z and t are respectively

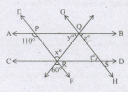
(a)
60°, 75°, 75°, 60°
(b)
50°, 75°, 75°, 65°
(c)
60°, 70°, 60°, 70°
(d)
60°,60°, 70°, 70°

Solution :

x° = 60° (vertically opposite)
x = y (acute angle)
⇒ y = 60°

= 180° - (60° + 50°)
t = 70°
Also, t = z = (acute angle)
x = 70°

23 )

In an equilateral triangle with side a, altitude and is

(a)
\({\sqrt{3a}\over2},{\sqrt3\over2}a\)
(b)
\({\sqrt{3a}\over4},{\sqrt3\over4}a^2\)
(c)
\({\sqrt3\over 2}a,{\sqrt3\over 4}a^2\)
(d)
none of.these

Solution :

Since it is equilateral trainqle with side 'a'
AB=AC=BC=a
DrawAD ⊥ BC
In ΔADB and ΔADC, we have
AB = AC (given) \(\lfloor B=\lfloor C=60^0\)

ΔADB ≅ ΔADC
From right ΔADB, we have
AB² = AD² + BD² (by Pythagoras)
\(AD^2=a^2-{a^2\over 4}={3a^2\over 4}\)
\(AD={\sqrt3\over 2}a=\)altitude
Area of ΔABC =\(1\over2\) x base x altitude
=\(1\over2\) x BC x AD
\(={1\over 2}\times a \times{\sqrt3\over 2}a={\sqrt3\over 4}a^2\)sq.units
Area \(ΔABC=\left( {\sqrt3\over 4}a^2\right)sq.units\)

24 )

The length of the diagonals of a rhombus are 6 cm and 8 cm. Find the length of each side of the rhombus

(a)
2cm
(b)
3cm
(c)
4cm
(d)
5cm

Solution :

We know, diagonals of a rhombus bisect and are perpendicular to each other.
Length of each side = \(\sqrt{\left(8\over2 \right)^2+\left(6\over 2 \right)^2}=5cm\)

25 )

The sides BA and DC of quadrilateral ABCD are produced as shown. Then which of following is correct

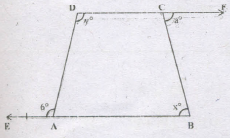
(a)
2x⁰+y⁰=a⁰+b⁰
(b)
\(x^0+{1\over2}y^0={a^0+b^0\over 2}\)
(c)
x⁰+y⁰=a⁰+b⁰
(d)
a⁰+b⁰=x⁰+y⁰

Solution :

\(\lfloor A+b^0=180^0\)
\(\lfloor A=180^0-b^0\)
Also \(\lfloor C+a^0=180^0-b^0\)
\(\Rightarrow\lfloor c=180^0-a^0\)
But \(\lfloor A^0+\lfloor B^0+\lfloor C^0+\lfloor D^0=360^0\)
⇒(180⁰- b⁰) + x⁰ + (180⁰ - a⁰) + y⁰ = 360⁰
⇒ x⁰ + y⁰ = a⁰ + b⁰

26 )

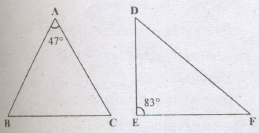
If ΔABC and 6.DEF are similar triangles in which \(\lfloor A=47^0\) and \(\lfloor E=83^0\), then \(\lfloor C\) is

(a)
50⁰
(b)
20⁰
(c)
60⁰
(d)
80⁰

Solution :

Since ΔABC - ΔDEF
\(\lfloor B=\lfloor E=83^0\)
Hence, in ΔABC, \(\lfloor A+\lfloor B+\lfloor C=180^0\)
\(\Rightarrow\lfloor C =180^0-(47^0+83^0)=50^0\)

27 )

In a simultaneous throw of a pair of dice, find the probability of getting a total more than 7?

(a)
\(\frac{4}{5}\)
(b)
\(\frac{1}{12}\)
(c)
\(\frac{5}{12}\)
(d)
none of these

Solution :

Here n{S)={6x 6)=36
Let E=Event of getting a total more than 7
= {{2,6) (3,5) (3,6) (4,4) (4,5) (4,6) (5,3) (5,4) (5,5) (5,6) (6,2) (6,3) (6,4) (6,5) (6,6)}
\(\therefore P(E)=\frac{n(E)}{n(S)}=\frac{15}{36}=\frac{5}{12}\)

28 )

If three metallic spheres of radii 6 cm, 8 cm and 10 cm are melted to form a single sphere, the diameter of the new sphere will be

(a)
12 cm
(b)
24 cm
(c)
30 cm
(d)
36 cm

Solution :

Volume of New Sphere
\(=\left[ \frac { 4 }{ 3 } \pi \times { (6) }^{ 3 }+\frac { 4 }{ 3 } \pi \times { (8) }^{ 3 }+\frac { 4 }{ 3 } \pi \times { (10) }^{ 3 } \right] { cm }^{ 3 }\)
\(=\left[ \frac { 4 }{ 3 } \pi ({ (6) }^{ 3 }+{ (8) }^{ 3 }+{ (10) }^{ 3 } \right] { cm }^{ 3 }\)
\(=\left[ \frac { 4 }{ 3 } \pi \times 1728 \right] { cm }^{ 3 }={ \left[ \frac { 4 }{ 3 } \pi \times { (12) }^{ 3 } \right] { cm }^{ 3 } }\)
Let the radius of the new sphere be R. Then,
\(\frac { 4 }{ 3 } \pi { R }^{ 3 }=\frac { 4 }{ 3 } \pi { (12) }^{ 3 }\Rightarrow R=12cm\)
Diameter = 2R=24cm

29 )

The distance between two points of a line segment is called

(a)
Point of the line segment
(b)
Collinear
(c)
Length of the line-segment
(d)
none of these

30 )

A figure consisting of two rays with end points is called an

(a)
Line
(b)
Point
(c)
Plane
(d)
Angles

31 )

If the sum of two angles is 180°, they are _______ to each other

(a)
Complimentary
(b)
Right angle
(c)
Supplementary
(d)
none of these

32 )

When two dice are rolled together, the probability of getting an even number on one dice and a multiple of 3 on the other is

(a)
\(\frac{1}{6}\)
(b)
\(\frac{7}{36}\)
(c)
\(\frac{4}{9}\)
(d)
\(\frac{5}{36}\)

Solution :

Total number of outcomes =36 favorable outcomes
={(2,2) (3,2) (2,6) (6,2) (4,3) (3,4) (6,6)}
Thus, P(even number on one and multiple of 3 on another) =\(\frac{7}{36}\)

33 )

How many face cards are there in a deck of playing cards?

(a)
4
(b)
3
(c)
12
(d)
13

Solution :

Number of face cards in a deck of playing cards 4(Jacks) +4(Queens) +4(Kings)= 12

34 )

If each edge of a cube is doubled, then the volume:

(a)
is doubled
(b)
becomes 4 times
(c)
becomes 6 times
(d)
becomes 8 times

Solution :

Let original edge = a. Then, volume = a³
New edge = 2a. So, new volume = (2a)³=8a³
∴ Volume becomes 8 times

35 )

Which of the following is true. where AD is the altitude
to the hypotenuse of a right angled ΔABC?

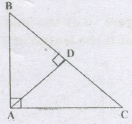
I.ΔABD ~ ΔCAD
II.ΔABD ~ ΔCDA
Ill.ΔABD ~ ΔCAB
of these above statemC!1ts, the correct ones arc combination of

(a)
I and II
(b)
I and III
(c)
II and III
(d)
I, II and III

Solution :

I. In ΔABD and ΔCAD, as each
ΔADB ~ ΔCAD
II. In Δ ABD and ΔCDA each
and AD = AD (common)
ΔABD ≅ ΔCDA
III. In AADBand ACAB

\(\lfloor B=\lfloor B\)
ΔADB ~ ΔCAB
Hence, I, II, III are correct statements.

36 )

In figure ∠AOC and ∠BOC form a linear pair.Then the value of x is

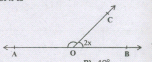
(a)
15°
(b)
40°
(c)
25°
(d)
30°

Solution :

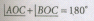
4x + 2x = 180° ⇒ 6x = 180° ⇒ x = 30°

37 )

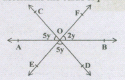
In figure, determine the value of y

(a)
25°
(b)
35°
(c)
15°
(d)
40°

Solution :

Here; as OA and OB are opposite rays,

5y + 5y +2y = 180°
12y = 180° Y = 15°

38 )

Cards each marked with one of the numbers 4, 5, 6 .... 20. are placed in a box and mixed thoroughly. One card is drawn at random from the box, what is the probability of getting an even number?

(a)
0
(b)
1
(c)
-1
(d)
\(\frac{1}{2}\)

Solution :

Number of favourable outcomes = 0 as the only even prime number is 2 which is not include in the given numbers.

39 )

What is the probability of getting 53 Sundays in an ordinary year?

(a)
\(\frac{1}{7}\)
(b)
\(\frac{2}{7}\)
(c)
\(\frac{1}{365}\)
(d)
\(\frac{1}{366}\)

Solution :

There are seven days in a week 52 x 7=364
365-364=1
This remaining 1 day may be anyone of the seven days of the week
∴ Required probability = \(\frac{1}{7}\)

40 )

ABC and DBC are two right triangles with common hypotenuse BC and' with their sides AC and DB intersecting at P. then product of AP.PC is equal to product of

(a)
BD.AB
(b)
PD.AP
(c)
PC.BP
(d)
BP.PD

Solution :

=(each = one right angle)
:. Points B, A, D, Care concyclic
(angles on the same side of segment BC are equal)
AP.PC ==BP.PD (products of segments of intersecting chords of a circle)

41 )

In the given figure, the angle A of the triangle ABC is a right angle. The circle on AC as diameter cuts BC at D. If BD=9, DC=7, calculate the length of AB.

(a)
14
(b)
13
(c)
11
(d)
12

Solution :

Since OA is a radius, = 90^o, BA is the tangent to the circle, by the tangent radius property
Hence, BA²=BDxBC ==9x 16==144
=> BA =12

42 )

If the diagonals of the quadrilateral ABCD cut at 0, and if OA=3 em, OB=9 cm, AC=15 cm, BD=13 cm. Then ABCD is

(a)
Parallel to each other
(b)
Equal
(c)
Cyclic
(d)
none of these

Solution :

OC=AC - OA=15 - 3=12 cm
OO=BD - BO=12 - 9=4 cm
:. AO.OC=3 x 12=36 cm²
BO.OD=9 x 4=36 cm²
=> AO - OC=BO - OD
Hence, ABCD is a cyclic quadrilateral

43 )

A circle is inscribed in quadrilateral ABCD.If BC=38 cm BQ=27 cm, DC=25 cm and AD^{\(\bot \)}BC. Find the radius of the circle

(a)
7 cm
(b)
15 cm
(c)
14 cm
(d)
none of these

Solution :

Let the sides AD, AB. BC and CD touch the circle at point P, Q. R, S respectively.
Since, tangent to a circle is perpendicular to the radius through the point of contact.
:. OP^{\(\bot \)}AD and OS^{\(\bot \)}DC. Also AD^{\(\bot \)}DC (given)
.'. OPDS is a square
BR=BQ=27cm (tangents from an external point to a circle are equal in length)
CR=HC-BR=(38-27)cm = 11 cm
Similarly, CS=CR=1 cm
DS=DC-CS=(25-11) cm =14 cm
Radius of circle = OP =OS = 14 cm
(.'. OPDS is a square)

44 )

About the number of pairs which have 16 as their HCF and 136 as their LCM,we can defiantly say that

(a)
No such pair exists
(b)
only one such pair exists
(c)
only two such pair exists
(d)
many such pair exists.

Solution :

Since, 16 is not a factor of 136, it follows that these does not exists any pair of number with HCF 16 and LCM136.

45 )

By what least number 4320 be multiplied to obtain a number which is a perfect cube?

(a)
20
(b)
30
(c)
40
(d)
50

Solution :

Clearly 4320 = 2³ \(\times\)3³\(\times\)2²\(\times\)5¹
To make it a perfect cube, it must be multiplied by
2 \(\times\) 5²i.e., 50

46 )

Find the area of a rhombus if its vertices are (3, 0) (4, 5) (-1,4) and (:-2, -1) taken in order.

(a)
34 sq units
(b)
24 sq units
(c)
20 sq units
(d)
44 sq units

Solution :

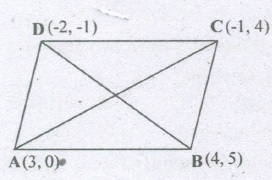
We know,
Area of a rhombus = \(\frac{1}{2}\)[product of its diagonals]
∴ Area of the rhombus ABCD =\(\frac{1}{2}\)(ACxBD)
\(=\frac{1}{2}[ (\sqrt{(-1-3)^{2}+{(4-0)^{2}}})+(\sqrt{(-2-4)^{2}{(-1-5)^{2}}})]\)
\(=\frac{1}{2}[(\sqrt{16+16})(\sqrt{36+36})]\)
\(=\frac{1}{2}(\sqrt{32})(\sqrt{72})=\frac{1}{2}(4\sqrt{2})(6\sqrt{2})\)
=24 square units

47 )

The mid-point of the line segment joining (2a, 4) and (-2, 3b) is (1, 2a+ 1). Find a and b value?

(a)
(2, -2)
(b)
(-2, 2)
(c)
(2, 2)
(d)
none of these

Solution :

Let the given points be A(2a, 4) and.B(-2, 3b)
∴ Co-ordinates of the mid-points of AB are \((\frac{2a-2}{2},\frac{4+3b}{2})\)
But given that the mid-point of AB is (1, 2a+ 1)
∴ \(\frac{2a-2}{2}\)=1 and \(\frac{4+3b}{2}\)=2a+1
⇒ 2a=4 and 4a-3b=2 ➝ (1)
⇒ a=2 substitute a=2 in ➝ (1)
8-3b=2
-3b=-6
b=2

48 )

Sidesoftwo similar triangles are in the ratio 4:9. Area of these triangles are in the ratio

(a)
2:3
(b)
4:9
(c)
81:16
(d)
16:81

Solution :

Ratio of areas = \(\left(4\over 9 \right)^2=16:81\)

49 )

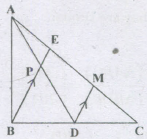
In figure, ΔABC, AD is a median of ΔABC. P is the mid-point of AD.Then ratio of AE and AC is

(a)
1:1
(b)
1:2
(c)
1:3
(d)
2:3

Solution :

In ΔCBE,
∵ D is the midpoint of BC and DM || BE
∴ M is the midpoint of EC
(By BasicProportionality Theorem)
∴ CM = ME ➝ (1)
In ΔADM,
∵ P is the midpoint of AD and PE || DM
∴ E is the midpoint of AM (By BPT)
∴ AE = EM ➝ (2)
From(1) and (2)AE=EM=CM
∴ \(AE={1\over 3}AC\)

50 )

The sides of a triangle are 6 cm, 8 cm and 10 cm. The largest angle of the triangle is

(a)
Acute angle
(b)
Right angle
(c)
Obtuse angle
(d)
Reflex angle

Solution :

∴ 6² + 8² = 10²
∴ By converse of Pythagoras Theorem
The angle between side of length 6 am and 8 cm = 90° which is the largest angle and a right angle,

51 )

If the sides of a triangle are 6 cm, 8 cm and 12 cm, then the nature of the triangle will be

(a)
Right angled
(b)
Obtuse angle
(c)
Acute angled
(d)
Not possible

Solution :

Let AB=6 cm, BC=8 cm and CA=12 cm. Then
CN² > AB² + BC²
\(∴\lfloor C\) is obtuse
∴ ΔABC is obtuse angled.

52 )

A is twice as good as workman as Band together they finish a piece of work in 18 days. In how many days will A alone finish the work?

(a)
25
(b)
26
(c)
27
(d)
none of these

Solution :

(A's 1 day work): (B's 1 day work) = 2 : 1
(A+B)'s 1day's work\(=\frac { 1 }{ 8 } \)
Divide\(\frac { 1 }{ 18 } \)in the ratio = 2: 1
A's 1 day's work\(=\left( \frac { 1 }{ 18 } \times \frac { 2 }{ 3 } \right) =\frac { 1 }{ 27 } \)
Hence, A alone can finish the work in 27 days.

53 )

If Sin(B+C-A) = Cos(C+A-B) = Tan(A+B-C)=1,then the angles A. B. Cwhich are positive acute angles are respectively

(a)
45⁰, 80⁰, 105⁰
(b)
22\(\frac{1}{2}\)⁰ , 62\(\frac{1}{2}\)⁰,45⁰
(c)
20⁰ , 70⁰ , 90⁰
(d)
30⁰ , 60⁰ , 90⁰

Solution :

Sin( B + C - A) = 1 = Sin90⁰
⇒ B + C - A = 90⁰ ⇾ (1)
⇒ Cos ( C + A - B) = 1= Cos0⁰ ⇢ (2)
Tan( A + B + C) = 1= Tan45⁰
⇒ A+B+C=45⁰ ⇢ (3)
Add (1), (2) and (3) we get,
A+B+C=135⁰ ⇢ (4)
Subtract (1), (2), (3) from (4) respectively, we get
2A = 45⁰,2B = 135⁰ ,2C = 90⁰
A=22 \(\frac{1}{2}\)⁰ ,B= 62\(\frac{1}{2}\)⁰,C=45⁰

54 )

If y=5, then what is the value of 10y \(\sqrt{y^1-y^2}\) ?

(a)
100
(b)
500
(c)
\(200\sqrt5\)
(d)
\(50\sqrt2\)

Solution :

\(10y\sqrt{y^2-y^2} \ 10 \times 5\sqrt{5^2-5^2}= 50 \times \sqrt{125-25}\)
\(=50 \times \sqrt{100}= 50 \times 10 =500\)

55 )

The point where a tangent line intersects a circle is called the

(a)
Centre
(b)
point of contact
(c)
end-point
(d)
none of these

56 )

Two circles of radii 5 cm and 3 cm touch each other internally, the distance between their centres is

(a)
5 cm
(b)
3 cm
(c)
2 cm
(d)
8 cm

Solution :

Distance = 5 cm - 3 cm = 2 cm

57 )

A(3, 2) and B(-2, 1) are two vertices of a triangle ABC, whose centroid G has a co-ordinate \((\frac{5}{3},\frac{1}{3})\) .Find the coordinates of the third vertex C of the triangle.

(a)
(-4,4)
(b)
(-4,-4)
(c)
(4,-4)
(d)
none

Solution :

A(3, 2) B(-2, 1)
Let the coordinates of the third vertex C of the triangle be (x, y)
Then
\(G(\frac{(3)+(-2)+(x)}{3},\frac{(2)+(1)+(y)}{3})\)
\(⇒ G(\frac{x+1}{3},\frac{y+3}{3})\)
But G is \((\frac{5}{3},\frac{-1}{3})\) (Given)
∴ \(\frac{x+1}{3} =\frac{5}{3}⇒x=4\)
\(\frac{y+3}{3}=\frac{-1}{3}⇒y=-4 \)
∴ C=(4,-4)

58 )

If TPand TQare the two tangents to a circle with centre O so that =100^o, then is equal to

(a)
60^o
(b)
80^o
(c)
50^o
(d)
120^o

Solution :

+= 180^o
\(\Rightarrow \)+100^o= 180^o
= 80^o

59 )

For what value(s) of x, the area of a triangle formed by the points (5, -1) (x, 4) and (6, 3) is 5.5 square units?

(a)
9 or \(\frac{7}{2}\)
(b)
-9 or \(\frac{7}{2}\)
(c)
9 or -\(\frac{7}{2}\)
(d)
none of these

Solution :

A(5. -1) B(x, 4) and C(6, 3)
Area of △ABC
\(=\frac{1}{2}\)S(4-3)+x(3 -(-1))+6( -1-4)]
\(=\frac{1}{2}\)[5+ 4x -30]
\(=\frac{1}{2}\)(4x-25)
If this area is 5.5 square units, then
\([\frac{1}{2}(4x-25)]=5.5\)
\(⇒ [\frac{1}{2}(4x-25)]=\frac{11}{2}\)
\(⇒ (4x-25)=11\)
⇒ 4x-25=11 i.e x=9
or 4x-25=-11 i.e x=\(\frac{7}{2}\)

60 )

The sum of all exterior angles of a convex polygon of n sides is

(a)
4 right angles
(b)
\(\frac2 n\)right angles
(c)
(2n-4) right angles
(d)
\(\frac n 2\)right angles

Solution :

Clearly sum of .all exterior angles of a convex polygon of n sides = 4 right angles

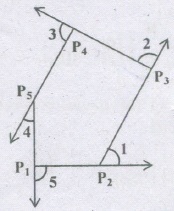
(\(\lfloor 1\)+\(\lfloor 2\)+\(\lfloor 3\)+\(\lfloor 4\)+\(\lfloor 5\)=4 right angles)

61 )

x = 1 - q and y = 2q + 1, then for what value of q, x is equal to y?

(a)
0
(b)
\(\frac{1}{2}\)
(c)
2
(d)
-1

Solution :

x = y ⇒ 1- q = 2q +1⇒ 3q = 0 ⇒ q = 0

62 )

The total number of prime factors in the expression
( 4)¹¹ \(\times\) ( 7)⁵\(\times\) (11)² is

(a)
30
(b)
29
(c)
28
(d)
31

Solution :

( 4)¹¹ \(\times\) ( 7)⁵\(\times\) (11)²=(2\(\times\)2)¹¹\(\times\) ( 7)⁵\(\times\) (11)²
=2¹¹ \(\times\) 2¹¹\(\times\) 7⁵ \(\times\) 11²
=2²² \(\times\) 7⁵ \(\times\) 11²
∴ Totalnumber of prime factors = 22 + 5 + 2 =29

63 )

What least value must be assigned to * so that the number 197 * 5462 is divisible by 9?

(a)
3
(b)
2
(c)
4
(d)
5

Solution :

Let the missing digit be x
To check divisibility by 9,
digit sum should be equal to 9
i.e.197x5462 = 1+9+7+x+5+4+6+2
= (34+x)
Digitsumof34 = 3+4=7
Now,(7+x). Hence to get 9, x=2
The digit is place of * must be 2

64 )

The last digit of the number (196)⁴²⁴

(a)
6
(b)
7
(c)
8
(d)
9

Solution :

Last digit of (1096)⁴²⁴
⇒ 6⁴²⁴=6^4k=6 ; (k = 106)

65 )

An inspector of school wishes to distribute 84 balls and 180 balls equally among a number of boys find the greatest number receiving the gift

(a)
6
(b)
12
(c)
18
(d)
7

Solution :

HCF (84,180) = 12

66 )

The area of the triangle whose vertices are (0, 0) (a, 0) and (0, b) is

(a)
ab
(b)
\(\frac{1}{2}ab\)
(c)
a+b
(d)
a²+b²

Solution :

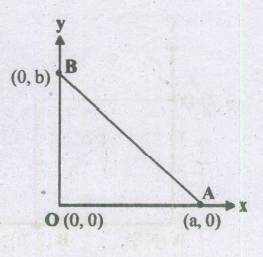
Area = \(\frac{ab}{2}\)

67 )

The coordinates of the point, dividing the join of the points (5, 0) and (0,4) in the ratio 2:3 internally are

(a)
\((3,\frac{8}{5})\)
(b)
\((1,\frac{4}{5})\)
(c)
\((\frac{5}{2},\frac{3}{4})\)
(d)
\((2,\frac{12}{5})\)

Solution :

\(x=\frac{2(0)+3(5)}{2+3}=3\)
\(y=\frac{2(4)+3(0)}{2+3}=\frac{8}{5}\)

68 )

Rs. 1 and Rs. 5 coins are available (as many requireD).
Find the smallest payment which cannot be made by these coins, if not more than 5 coins are allowed.

(a)
3
(b)
14
(c)
12
(d)
18

Solution :

14 is the required number, because
14 = 5+5+1+1+1+1
Here, for the payment of~ 14 six coins are required.
So, we cannot make payment of Rs.14, by given coins

69 )

A man can row upstream at 7 kmph and downstream at 10 kmph. Find man's rate in still water and the rate of current.

(a)
8.5 krn/hr, 2 krn/hr
(b)
8.5 km/hr, 1.5 km/hr
(c)
7.5 km/hr, 2.5 km/hr
(d)
none of these

Solution :

Rate in still water\(=\frac { 1 }{ 2 } \left( 10+7 \right) \) km/hr = 8.5 km/hr
Rate in current\(=\frac { 1 }{ 2 } \left( 10-7 \right) \) km/hr = 1.5 km/hr

70 )

The sum of the numerator and the denominator of a fraction is 12. If the denominator is increased by 3, the fraction becomes \(1\over 2\).Find the fraction.

(a)
\(3\over 7\)
(b)
\(2\over 7\)
(c)
\(4\over 7\)
(d)
\(5\over 7\)

Solution :

Lethe required fraction be \(x\over y\) . Then
x +y = 12 ⟶ (1) and
\({{x\over y+3}}={1\over 2} ⇒ 2x = Y + 3 ⇒ 2x - y = 3 ⟶ (2)\)
Add (1) and (2) we get
3x = 15 ⇒ x = 5
Substitutex = 5 in (l) we get
5+y=12 ⇒ y=12-5=7
x = 5,Y= 7. Hence, the required fraction \(={5\over 7}\)

71 )

90% and 97% pure acid solutions are mixed to obtain 21litres of 95% pure acid solution. Find the quantity of each type of acid to be mixed to form the mixture.

(a)
5, 15
(b)
6, 14
(c)
5, 15
(d)
none of these

Solution :

Let the given solution -be labelled as A and B respectively
Let x litres of A be mixed with y litres of B
Then x+ y =21 ⟶ (1)
Quantity of acid in x litres of A = (90% of x) litres
\(=\left(x\times{90\over 100} \right)\) litres =\({9x\over 10}\)litres
Quantity of acid in y litres of B = (97% of y) litres
\(=\left(y\times{90\over 100} \right)\)litres =\({9y\over 10}\)litres
Quantity of acid in 21 litres of (A+ B)
= 95% of 21 litres=\(\left(21\times{95\over 100} \right)\)litres \({399\over 20}\)litres
\({9x\over 10}+{97y\over 100}={399\over 20}⇒90x+97y=1995⟶(2)\)
Multiplying (1) by 90 and subtracting the result from (2)
Weget 7y=105 ⇒ y=15
Substitute y = 15 in (1). we get x+ 15 = 21
⇒ x=6
∴ x=6,y=15
So, 6 litres of 90% solution is mixed with 15 litres of 97% solution.

72 )

For what value ofk, the system of equations 2x + ky = 1, 3x - 5y = 7, has no solutions?

(a)
\(k={-10\over 3}\)
(b)
\(k={10\over 3}\)
(c)
\(k={3\over 10}\)
(d)
none of these

Solution :

\({2\over 3}={k\over -5}\neq{1\over 7}⇒k={-10\over 3}\)

73 )

Find the value of a so that the point (3, a) lies on the line represented by 2x - 3y = 5

(a)
1
(b)
3
(c)
1/3
(d)
-1/3

Solution :

2(3) -3a = 5
-3a = 5-6
-3a =-1
\(a={1\over 3}\)

74 )

The point A{5, -1) on reflection is x-axis is mapped as A'. Also A 3n reflection in V-axis is mapped as A". Write the coordinates of A' and A" and calculate the
distance of A'A".

(a)
3\(\sqrt{26}\)units
(b)
2\(\sqrt{26}\)units
(c)
2\(\sqrt{-26}\)units
(d)
none of these

Solution :

A (5, -1) on reflection in x-axis is mapped onto A^' (5, 1)
A (5, -1) on reflection in y-axis is mapped onto A^'' (-5, -1)
∴ Distance between A^' and A^''
\(=A^{'}A^{''}=\sqrt{(-5-5)^{2}+{(-1+1)^{2}}}\)
=\(\sqrt{100+4}=\sqrt{104}=2\sqrt{26}\) units

75 )

Theclosedfigure with vertices (-2, 0) (2, 0) (2, 2) (O, 4) and(-2, 2) is a

(a)
Triangle
(b)
Quadrilateral
(c)
Hexagon
(d)
Pentagon

Solution :

Number of points (vertices) = 5
∴ Pentagon.

76 )

cos\((\frac{\pi}{2}-30°)\)is equal to

(a)
\(\frac{1}{\sqrt{3}}\)
(b)
\(\frac{1}{\sqrt{2}}\)
(c)
\(\frac{1}{2}\)
(d)
\(\frac{\sqrt{3}}{2}\)

Solution :

cos\((\frac{\pi}{2}-30°)\)=sin30°=\(\frac{1}{2}\)

77 )

If cotθ=\(\frac{b}{a}\) , then value of \(\frac{cosθ+sinθ}{cosθ-sinθ}\) is

(a)
\(\frac{b-a}{b+a}\)
(b)
b-a
(c)
b+a
(d)
\(\frac{b+a}{b-a}\)

Solution :

\(\frac{cosθ+sinθ}{cosθ-sinθ}=\frac{cotθ+1}{cotθ-1}=\frac{\frac{b}{a}+1}{\frac{b}{a}-1}=\frac{b+a}{b-a}\)

78 )

The arithmetic mean of the scores of a group of students in a test was 52. The brightest 20% of them secured a mean score of 80 and the dullest 25% a mean score of 31. The mean score of remaining 55% is

(a)
45
(b)
50
(c)
51.4 approx
(d)
54.6 approx

Solution :

Let the required mean score be x. Then
20 x 80 + 25 x 31 + 55 x x=52 x 100
⇒ 1600+775+55x=5200
⇒ 55x=2825 ⇒ x=51.4

79 )

Three years ago, the average age of A and B was 18years with C joining them, the average age becomes 22 years. How old is C now?

(a)
24 years
(b)
27 years
(c)
28 years
(d)
30 years

Solution :

Present age of (A+ B)=(18 x 2 + 3 x 2) years
=42 years
Present age of (A+B+C)=(22 x 3) years
=66 years
∴ C's age=(66-42) years=24 years

80 )

The modal value of a series is

(a)
middle most value
(b)
value whose frequency is maximum
(c)
value whose frequency is minimum
(d)
limiting value

81 )

The mean of first n natural number is

(a)
\(\frac { n+1 }{ 2 } \).
(b)
\(\frac { n(n+1) }{ 2 } \)
(c)
\(\frac { n(n-1) }{ 2 } \)
(d)
n²

Solution :

Mean =\(\frac { 1+2+3+....n }{ 2n } \)
= \(\frac { n(n+1) }{ 2n } =\frac { n+1 }{ 2 } \).

82 )

The average of 11 results is 60. If the average of first six results is 58 and that of the last six are 63. Find the sixth result.

(a)
46
(b)
56
(c)
66
(d)
none of these

Solution :

Sixth result=(58 x 6 + 6 x 63 - 60 x 11)=66

83 )

There are two temples, one on each bank of a river,just opposite to each other. One temple is 54m high. From the top of this temple, the angles of depression of the top and the foot of the other'temple are 30° and 60° respectively. Find the width of the river and the height of the other temple.

(a)
31.14 m, 18 m
(b)
11.14 m, 18 m
(c)
21.14 m, 17 m
(d)
none of these

Solution :

Let AB and CD be the two temples and AC be the river
Then, AB = 54 m

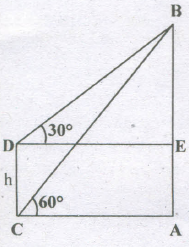
Let AC=x metres and CD=h metres
\(\angle ACB=60°,\angle EDB=30°\)
\(\frac { AB }{ AC } =Tan60°=\sqrt { 3 } \)
\(\Rightarrow AC=\frac { AB }{ \sqrt { 3 } } =\frac { 54 }{ \sqrt { 3 } } =\left( \frac { 54 }{ \sqrt { 3 } } \times \frac { \sqrt { 3 } }{ \sqrt { 3 } } \right) =18\sqrt { 3 } m\)
DE=AC=18\(\sqrt { 3 } m\)
\(\frac { BE }{ DE } =Tan30°=\frac { 1 }{ \sqrt { 3 } } \)
\(\Rightarrow BE=\left( 18\sqrt { 3 } \times \frac { 1 }{ \sqrt { 3 } } \right) =18m\)
\(\therefore\) CD = AE = AB - BE = (54 - 18)m = 36m
So, width of the river
=AC=\(18\sqrt { 3 } m\)=(1.8\(\times\)1.73)m = 31.14m
Height of the other temple = CD = 18 m

84 )

A man standing on the bank of a river observes that the angle subtended by a tree on the opposite bank is 60°. When he retires 36m from the bank, he finds the angle to be 30°. Find the breadth of the river.

(a)
15 m
(b)
16 m
(c)
17 m
(d)
18 m

Solution :

Let AB be the tree and AC be the river.
Let C and D be the two positions of the man.
Then, \(\angle ACB=60°,\angle ADB=30°,CD=36m\)

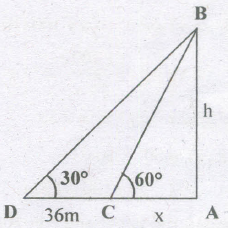
Let AB = h metres and AC = x metres
Then, AD = (36+x)m
\(\frac { AB }{ AD } =Tan30°=\frac { 1 }{ \sqrt { 3 } } \Rightarrow \frac { h }{ 36+x } =\frac { 1 }{ \sqrt { 3 } } \)
\(\Rightarrow h=\frac { 36+x }{ \sqrt { 3 } } ....(1)\)
\(\frac { AB }{ AC } =Tan60°=\sqrt { 3 } \Rightarrow \frac { h }{ x } =\sqrt { 3 } \Rightarrow h=\sqrt { 3 } x.....(2)\)
From (1) and (2) we get, \(\frac { 36+x }{ \sqrt { 3 } } =\sqrt { 3 } x\Rightarrow x=18m\)
so, breadth of the river = 18 m

85 )

After getting two successive discounts, a shirt with a list price of Rs.150 is available at Rs.105. If the second discount is 12.5%, find the first discount

(a)
10%
(b)
5%
(c)
20%
(d)
none of these

Solution :

Let the first discount = x%
Then, 87.5% of (l00 -x)% of 150 = 105
\(\Rightarrow\)\(\frac{87.5}{100}\times\frac{(100-x)}{100}\times\)150=105
\(\Rightarrow\)100-x =\(\left( \frac { 105\times 100\times 100 }{ 150\times 87.5 } \right) \)=80
\(\Rightarrow\)x = 100 - 80 = 20
\(\therefore\)First discount =- 20%

86 )

A discount dealer professes to sell his goods at cost price but uses a weight of 960 grams for a kg weight. Find his gain percent?

(a)
\(3\frac{1}{6}\)%
(b)
\(4\frac{1}{6}\)%
(c)
\(5\frac{1}{6}\)%
(d)
none of these

Solution :

Gain%=\(\left[ \frac { Error }{ (True\quad value)-(Error) } \times 100 \right] \)%
=\(\left( \frac { 40 }{ 960 } \times 100 \right) \)%=\(4\frac{1}{6}\)%

87 )

Inthegivenfigure, PP' and QQ'

(a)
Perpendicular
(b)
Parallel
(c)
equal
(d)
none

Solution :

Produce PP' and QQ' to meet at a point A.

Since, the lengths of tangents to a circle from a point outside it are equal.
We have, PA=QA^{\(\rightarrow \)}(1)
and P'A=Q'A^{\(\rightarrow \)}(2)
From (1) and (2), we get PA-P'A=QA-Q'A
.'. PP'=QQ' .'. ie. PP' and QQ' are equal

88 )

Find the length of the arc in the following figure.

(a)
11 cm
(b)
22 cm
(c)
33 cm
(d)
44 cm

Solution :

Length of arc = \(2\times \frac { 22 }{ 7 } \times 21\times \frac { 60^{ o } }{ { 360 }^{ o } } =22 cm\)

89 )

What is the supplementary angle of the central angle of a semicircle?

(a)
0^o
(b)
90^o
(c)
180^o
(d)
360^o

Solution :

Central angle of a semi-circle =\(\frac { { 360 }^{ o } }{ 2 } \)=180^o
.'. Its supplementary angle = 180°-180°=0°

90 )

If 3x-5y=5 and \(\frac{x}{x+y} = \frac{5}{7}\), then what is the value of x-y?

(a)
9
(b)
6
(c)
4
(d)
3

Solution :

3x - 5y = 5 ⇾ (1)
\(\frac{x}{x+y}=\frac{5}{7} \Rightarrow\) 7x = 5x + 5y
\(\Rightarrow\) 2x - 5y = 0 ⇾ (2)
Subtract (2) from (1). we get x = 5
Putting x = 5 in (1), we get y = 2,
so x-v = 5-2 = 3

91 )

The mean proportional between 234 and 104 is

(a)
54
(b)
39
(c)
12
(d)
156

Solution :

Required mean proportional = \(\sqrt{234 \times 104}\)
\(=\sqrt{13 \times 9 \times 2 \times 13 \times 8}\)
= 13 x 3 x 4 = 156

92 )

A number is 729 times the square of its reciprocal. The number is

(a)
9
(b)
4
(c)
3
(d)
2

Solution :

\(x = 729,\frac{1}{x^2}\)
x³ = 729 ⇒ x =9

93 )

What must be subtracted from 2x⁴-11x³ + 29x²-40x+29, so that the resulting polynomial is exactly divisible by x²-3x+4?

(a)
2x+5
(b)
-2x+5
(c)
3x+5
(d)
-3x+5

Solution :

94 )

Find the simple interest on Rs.3000 at \(6\frac{1}{4}\)% per annum for the period from 4^th February 2013 to 18th April 2013

(a)
27.50
(b)
37.50
(c)
17.50
(d)
none of these

Solution :

Time = (24 + 31 + 18) days = 73 days
=\(\frac{73}{365}\)years =\(\frac{1}{5}\)year
P=Rs.3000:R=\(6\frac{1}{4}\)%p.a=\(\frac{25}{4}\)%p.a
\(\therefore\)S.I=Rs.\(\left( 3000\times \frac { 25 }{ 4 } \times \frac { 1 }{ 5 } \times \frac { 1 }{ 100 } \right) \)=37.50

95 )

In the adjoining figure, ^{\(\Delta \)}ABC, Circumscribes a circle. Find the length of BC.

(a)
6 cm
(b)
8 cm
(c)
10 cm
(d)
12 cm

Solution :

BC = BP + PC = BR + CQ
=3 +(AC-AQ)
=3 +AC-AR
=3+11-4 = 10 cm

96 )

Find the value of a²+b²+2ab if a = -1, b = 3

(a)
4
(b)
5
(c)
6
(d)
3

Solution :

a²+b²+2ab is
a = -1, b = 3
(-1)²+(3)²+2(-1)(3) = 1 + 9 - 6
= 10 - 6
= 4

97 )

If a^x=b³, b^y=c³, c^z=a³ , then the value of xyz will be

(a)
0
(b)
9
(c)
27
(d)
can't be determined

Solution :

a^x = b³
(a^x)^y = (b³)y
a^xy = b^3y
⇒ a^xyz = [(c³)³]^z
= a^xyz = (c^z)⁹ = a²⁷

98 )

If x²-7x+10 is a factor of x⁴-px²+q, then the values of p and q respectively will be

(a)
29, 100
(b)
28, 10
(c)
29, 10
(d)
none of these

Solution :

x²-7x+10 = x²-5x-2x+10
⇒ x(x-5)-2(x-5)
x²-7x+10 = (x-2) (x-5)
f(x) = x⁴-px²+q
f(2) = (2)⁴-p(2)²+q
= 16-4p+q
4p-q =16 ⇾ (1)
and
f(5) = (5)⁴-p(5)²+q
= 625-25p+q
25p-q = 625 ⇾ (2)
Solving (1) and (2)
4p-q=16 ...(1)
\(\frac{25p-q=625}{-21p=-609}\Rightarrow p=29;\) ...(2)
4p-q = 16
4(29)-q = 16
116- q = 16 ⇒ -q = 16-116
-q = -100 ⇒ q = 100

99 )

In a \(\triangle ABC,\)

(a)
70^o
(b)
60^o
(c)
80^o
(d)
none of these

Solution :

We know, sum of angles of a triangle is 180^o

100 )

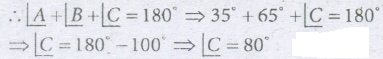
The difference between the interior and exterior angles of a regular polygon is 60^o. The number of sides in the polygon is

(a)
1
(b)
6
(c)
5
(d)
8

Solution :

Here interior angle - exterior angle =60^o
\(\frac{(n-2)\times180}{n}-\frac{360}{n}=60\)
\(\frac{1}{n}[(n-2)\times180-360]=60\)
\(\frac{1}{n}[180n-360-360]=60\)
\(\frac{1}{n}[180n-720]=60\Rightarrow180n-720=60n\)
180n-60n=720
120n=720
\(n=\frac{720}{120}=6\)

NTSE General English - Passage Completion Important Questions with Answer

NTSE General English - Fill in the Blanks Important Questions with Answer

NTSE General English - Cloze Test Sample Questions with Answer

NTSE General English - Sentence Rearrangements Practice Questions

NTSE General English - Sentence Completion Important Questions with Answer

NTSE General English - Error Detection Sample Practice Questions

NTSE SAT Geography - Transport Lifelines of National Economy Important Questions with Answer

NTSE SAT Geography - Population Sample Questions with Answer

NTSE SAT Geography - Resources and Development Important Questions with Answer

NTSE SAT Mathematics Sample Questions with Answer

SAT Mathematics

Exam Duration: 120 Mins Total Questions : 100

Latest Scholarship Exams Posts

NTSE General English - Connectors Sample Questions with Answer

Other Scholarship Exams Packs

Other Sub category

Online Practice Test

Scholarship Exams

NMMS மனத்திறன் தேர்வு

Scholarship Exams

NMMS அறிவியல்

Scholarship Exams

NMMS கணிதம்

Scholarship Exams

NMMS சமூக அறிவியல்

Scholarship Exams

NMMS வரலாறு History

Scholarship Exams

OTI365 - NTSE - X Standard

Scholarship Exams

NTSE - X Standard

Are you interested OTI365 - NTSE - X Standard Exam