Home
School Exams
Scholarship Exams
OTI365 - NTSE - X Standard
NTSE SAT Mathematics - Statistics Sample Question Paper

SAT Mathematics - Statistics

Exam Duration: 45 Mins Total Questions : 30

1 )

The formula for finding mode in a grouped frequency distribution is \(1+\left( \frac { { f }_{ 1 }-{ f }_{ 0 } }{ 2{ f }_{ 1 }-{ f }_{ 0 }-{ f }_{ 2 } } \right) \times h\) What does f₁ represent here?

(a)
frequency of the modal class
(b)
frequency of the class preceding the modal class
(c)
frequency of the class succeeding the modal class
(d)
frequency of the last class

2 )

The formula for finding out the median in a grouped frequency distribution is \(1+\frac { \left( \frac { n }{ 2 } -f \right) }{ f } \times h\) What does f represent here?

(a)
frequency of the class preceding the median class
(b)
cumulative frequency of the class preceding the median class
(c)
frequency of the class succeeding the median class
(d)
cumulative frequency of the class succeeding the median class

3 )

The weight of 12 men are given as 75, 73, 73, 72, 72, 72, 70, 70, 68, 68, 68, 68, kg. Find the mean weight?

(a)
70.75 kg
(b)
70.75 g
(c)
71.75 kg
(d)
none of these

4 )

Determine the mean of the following

Group	10-16	16-22	22-28	28-34	34-40
Frequency	1	10	5	3	6

(a)
24.72
(b)
25.77
(c)
25.72
(d)
none of these

5 )

Following is the distribution of earnings of 200 workers in a flour mill:

Monthly wages (in rupees)	80-100	100-120	120-140	140-160	160-180
No.of workers	20	30	20	40	90

Estimate the average earnings of the workers

(a)
115
(b)
125
(c)
135
(d)
145

6 )

The average weight of A, B, Cis 45 kg. If the average weight of A and B be 40 kg and that of B and C be 43 kg, find the weight of B?

(a)
21 kg
(b)
20 kg
(c)
38 kg
(d)
31 kg

7 )

Which of the following relations true?

(a)
AM=HM
(b)
GM=AM=HM
(c)
AM<HM
(d)
AM≥GM≥HM

8 )

Calculate the median for the following?

Marks Obtained	No.of Students
Below 10	6
Below 20	15
Below 30	29
Below 40	41
Below 50	60
Below 60	70

(a)
35
(b)
45
(c)
55
(d)
none of these

9 )

If the AM as well as GM of two positive numbers is 4, what is their HM?

(a)
2
(b)
4
(c)
8
(d)
none of these

10 )

The arithmetic mean of the scores of a group of students in a test was 52. The brightest 20% of them secured a mean score of 80 and the dullest 25% a mean score of 31. The mean score of remaining 55% is

(a)
45
(b)
50
(c)
51.4 approx
(d)
54.6 approx

11 )

Three years ago, the average age of A and B was 18years with C joining them, the average age becomes 22 years. How old is C now?

(a)
24 years
(b)
27 years
(c)
28 years
(d)
30 years

12 )

After replacing an old member by a new member, it was found that the average age of five members of a club is the same as it was B years ago. What is the difference between the ages of the replaced and the new member?

(a)
2 years
(b)
4 years
(c)
8 years
(d)
15 years

13 )

Which class interval has minimum frequency in the following group?

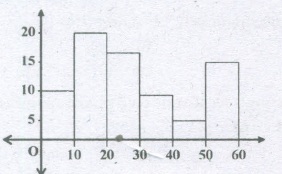
(a)
20-30
(b)
40-50
(c)
50-60
(d)
0-10

14 )

Which is the better measure of central tendency when individual observation are not important?

(a)
Mode
(b)
Median
(c)
Mean
(d)
none of these

15 )

Find the class marks of classes 10-25 and 33-55

(a)
10,35
(b)
25,55
(c)
15,20
(d)
17.5,45

16 )

The item value which occurs most frequently is called

(a)
Mean
(b)
Median
(c)
Mode
(d)
none of these

17 )

The class, whose cumulative frequency is greater than (and nearest to) n/2 is called

(a)
Average class
(b)
Median class
(c)
Modal class
(d)
Mean class

18 )

The algebraic sum of all the deviations of all the observations from their mean is always

(a)
0
(b)
+ve
(c)
-ve
(d)
equal to the number of observations

19 )

If mean = (3 median-mode) /k, then k=

(a)
1
(b)
1/2
(c)
2
(d)
none of these

20 )

Which of the following formulae is true for finding mean?

(a)
\(\bar { x } =\frac { \sum _{ i=1 }^{ n }{ { x }_{ i } } }{ n } \)
(b)
\(\bar { x } =\sum _{ i=1 }^{ n }{ \sum { x_{ i }^{ 2 } } } \)
(c)
\(\bar { x } =\frac { \sum _{ i=1 }^{ n }{ { x }_{ i } } }{ { n }^{ 2 } } \)
(d)
\(\bar { x } =\frac { \sum _{ i=1 }^{ n }{ { x }_{ i }^{ 2 } } }{ { n }^{ 2 } } \).