Home
School Exams
Scholarship Exams
OTI365 - NTSE - X Standard
NTSE SAT Mathematics - Triangles Sample Questions with Answer

NTSE SAT Mathematics - Triangles

Exam Duration: 45 Mins Total Questions : 30

1 )

Sides of triangles are given below, the triangle is (2a.- 1) cm, 2√2a cm and (2a + 1) em

(a)
Obtuse
(b)
Acute
(c)
Equilateral
(d)
Right angled.

Solution :

Let p = (2a - 1)em,q = 2√2a em,
r = (2a + I)em
(p² +q²) = (2a-I)² cm² + (2√2a)² cm²
= [( 4a² + 1- 4a) + 8a] em 2
= ( 4a² + 4a + 1)cm²
= 2a + 12 cm² = r²
(p² + q²) = r²
The given triangle is right angled

2 )

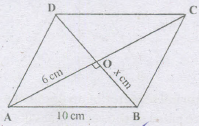
In a rhombus of side 10 em, one of the diagonals is 12 em long. Find the length of the second diagonal.

(a)
15cm
(b)
16cm
(c)
17cm
(d)
none

Solution :

Let AC= 12cm and BD=2x em
We know, diagonals of a rhombus bisect each other at right angles.
\(OA={1\over 2}AC=6cm\)
\(OB={1\over 2}BD=x\ cm\) and \(\angle{AOB}=\)90⁰
Fromright ΔAOB, wehave
AB² = OA² + OB²
OB² = [(10)² -(6)²]cm² =64 cm²
⇒ x² =64 cm² ⇒ x = 8 cm
BD=(2 x OB)=16 cm

3 )

In a quadrilateral ABCD, \(\lfloor B=90^0\)
If AD²+ BC² + CD², then

(a)
70⁰
(b)
80⁰
(c)
90⁰
(d)
none of these

Solution :

\(\lfloor B=90^0\)and
AD² = BC² + CD²
To find 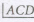Join AC
In ΔABC, \(\lfloor B=90^0\)
AC²= AB²+ BC² (By Pythagoras theorem)-(1)
Now, AD²=AB²+BC²+CD²(given)
⇒ AD²=AC² + CD²
Thus in ΔACD, we have AD² + CD²
Hence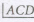 = 90⁰ (by converse of Pythagoras)

4 )

In an equilateral triangle with side a, altitude and is

(a)
\({\sqrt{3a}\over2},{\sqrt3\over2}a\)
(b)
\({\sqrt{3a}\over4},{\sqrt3\over4}a^2\)
(c)
\({\sqrt3\over 2}a,{\sqrt3\over 4}a^2\)
(d)
none of.these

Solution :

Since it is equilateral trainqle with side 'a'
AB=AC=BC=a
DrawAD ⊥ BC
In ΔADB and ΔADC, we have
AB = AC (given) \(\lfloor B=\lfloor C=60^0\)

ΔADB ≅ ΔADC
From right ΔADB, we have
AB² = AD² + BD² (by Pythagoras)
\(AD^2=a^2-{a^2\over 4}={3a^2\over 4}\)
\(AD={\sqrt3\over 2}a=\)altitude
Area of ΔABC =\(1\over2\) x base x altitude
=\(1\over2\) x BC x AD
\(={1\over 2}\times a \times{\sqrt3\over 2}a={\sqrt3\over 4}a^2\)sq.units
Area \(ΔABC=\left( {\sqrt3\over 4}a^2\right)sq.units\)

5 )

The length of the diagonals of a rhombus are 6 cm and 8 cm. Find the length of each side of the rhombus

(a)
2cm
(b)
3cm
(c)
4cm
(d)
5cm

Solution :

We know, diagonals of a rhombus bisect and are perpendicular to each other.
Length of each side = \(\sqrt{\left(8\over2 \right)^2+\left(6\over 2 \right)^2}=5cm\)

6 )

The sides of a triangle are 50 em. 78 cm and 11 Z cm. The smallest altitude is

(a)
20cm
(b)
30cm
(c)
40cm
(d)
50cm

Solution :

Semi - perimeter of a triangle
\(={50+78+112\over 2}={240\over 2}=120cm\)
Area of Δle=\(\sqrt{s(s-a)(s-b)(s-c)}\)
\(\sqrt{120(120-50)(120-78)(120-111)\over 2}\)
= 1680sq.cm
The altitude will be smallest when base is largest
\({1\over 2}\times112\times h=1680\Rightarrow h={1680\times2\over 45}=30cm\)

7 )

The sides BA and DC of quadrilateral ABCD are produced as shown. Then which of following is correct

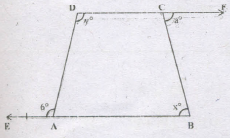
(a)
2x⁰+y⁰=a⁰+b⁰
(b)
\(x^0+{1\over2}y^0={a^0+b^0\over 2}\)
(c)
x⁰+y⁰=a⁰+b⁰
(d)
a⁰+b⁰=x⁰+y⁰

Solution :

\(\lfloor A+b^0=180^0\)
\(\lfloor A=180^0-b^0\)
Also \(\lfloor C+a^0=180^0-b^0\)
\(\Rightarrow\lfloor c=180^0-a^0\)
But \(\lfloor A^0+\lfloor B^0+\lfloor C^0+\lfloor D^0=360^0\)
⇒(180⁰- b⁰) + x⁰ + (180⁰ - a⁰) + y⁰ = 360⁰
⇒ x⁰ + y⁰ = a⁰ + b⁰

8 )

If and ΔCAB ~ ΔCED value of x is

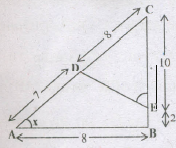
(a)
4cm
(b)
5cm
(c)
6cm
(d)
7cm

Solution :

As ΔCAB ~ ΔCED
\({CA\over CD}={CE\over DE}={CB\over CD}\)
So,\({AB\over DE}={CB\over CD}\therefore{9\over x}={10+2\over 8}\)
\(x={8\times9\over 12}=6cm\)

9 )

If ΔABC and 6.DEF are similar triangles in which \(\lfloor A=47^0\) and \(\lfloor E=83^0\), then \(\lfloor C\) is

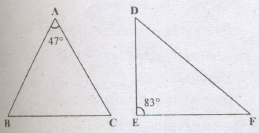
(a)
50⁰
(b)
20⁰
(c)
60⁰
(d)
80⁰

Solution :

Since ΔABC - ΔDEF
\(\lfloor B=\lfloor E=83^0\)
Hence, in ΔABC, \(\lfloor A+\lfloor B+\lfloor C=180^0\)
\(\Rightarrow\lfloor C =180^0-(47^0+83^0)=50^0\)

10 )

Which of the following is true. where AD is the altitude
to the hypotenuse of a right angled ΔABC?

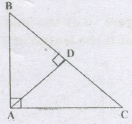
I.ΔABD ~ ΔCAD
II.ΔABD ~ ΔCDA
Ill.ΔABD ~ ΔCAB
of these above statemC!1ts, the correct ones arc combination of

(a)
I and II
(b)
I and III
(c)
II and III
(d)
I, II and III

Solution :

I. In ΔABD and ΔCAD, as each
ΔADB ~ ΔCAD
II. In Δ ABD and ΔCDA each
and AD = AD (common)
ΔABD ≅ ΔCDA
III. In AADBand ACAB

\(\lfloor B=\lfloor B\)
ΔADB ~ ΔCAB
Hence, I, II, III are correct statements.

11 )

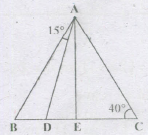
If in triangle BD=AO, AE=EC,then

(a)
95⁰
(b)
70⁰
(c)
65⁰
(d)
none of these

Solution :

BD = AD

AE = EC ⇒

⇒(15 + + 40)+15⁰+40⁰=180⁰
=70⁰

12 )

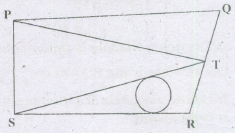
PQRS is a square of side 6 ern each and T is a mid-point of QR. What is the radius of circle inscribed in Δ TSR?

(a)
\(3\over 3-\sqrt5\)
(b)
\(6\over 3+\sqrt5\)
(c)
\(2\over 3+\sqrt5\)
(d)
none of these

Solution :

SR = 6 ; TR=3 (T is a mid-point)
\(ST=\sqrt{6^2+3^2}=3\sqrt5\)
Area of ΔSTR = r x s
where r=Radius of circle inscribed
s=semi-perimeter of triangle
\(⇒{1\over 2}\times3\times6=r\times\left(6+3+3\sqrt5\over2 \right)\)
\({18\over 9+3\sqrt5}=r={6\over 3+\sqrt5}\)

13 )

The perimeter of two timilar triangles is 30 cm and 20 cm. If one altitude of the former triangle is 12 ern, then length of the corresponding altitude of latter triangle is

(a)
8cm
(b)
10cm
(c)
12cm
(d)
15cm

Solution :

We know, the ratio of perimeter of two similar triangles are equal to the ratio of the corresponding altitudes of the two Δles.
\({30\over 20}={12\over length\ of\ the\ corresponding\ altitude of \ latter \Delta le}\)
⇒ length of the corresponding altitude of the
Δle = 8cm

14 )

The perimeter of two similar triangles is.40 em and 50 em.Then the ratio of the areas of the first and second triangles is

(a)
4:5
(b)
5:4
(c)
25:16
(d)
16:25

Solution :

∴ The ratio of areas of two similar Ales is equation to the square of the ratio of their corresponding perimeters.
∴ Ratio of the areas of the first and second triangles.
\(=\left(40\over 50 \right)^2=16:25\)

15 )

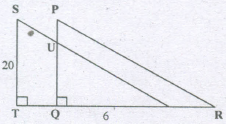
In given figure, U is the mid-point of SR and PQ= 8 units, what is the length of TQ?

(a)
4
(b)
12
(c)
8
(d)
6

Solution :

QR = 6 and PQ = 8 and \(\lfloor Q=90^0\)
⇒ PR=10 (using Pythagoras theorem)
ΔRUQ ~ ΔRST
(∵\(\lfloor R=\lfloor R\),(common) and

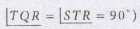
\({UQ\over ST}={RU\over RS}={RQ\over RT}\)

⇒ \({1\over 2}={6\over RT}⇒RT=12\) (using RU =US)
So, RT - RQ = TQ = 12 - 6 = 6

16 )

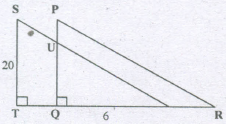
Aright triangle has hypotenuse of length p cm and side of length q cm. If p - q = 1, express the length the third side of the right triangle in term of p.

(a)
\(\sqrt{2p-1}cm\)
(b)
\(\sqrt{2p}cm\)
(c)
\(\sqrt{p-1}cm\)
(d)
none of these

Solution :

\(\lfloor B=90^0\)
AC= p cm
AB =q cm
Then. by Pythagoras theorem in ΔABC
AC²= AB² + BC²
p² = q² + BC²
BC² = p² - q²
⇒ BC² = p² - (p -1)² (∵ p-q = 1. q = p-1)
⇒ BC² = p² - (p² - 2 P + 1)
⇒ BC² = 2p - 1
BC = \(\sqrt{2p-1}\)

17 )

If one angle of a triangle is equal to one angle of the other triangle, and the sides including these angles are proportional, then the two triangles are similar. This criterion is known as

(a)
SSS similarity criterion
(b)
SAS similarity criterion
(c)
AA similarity criterion
(d)
AAA similarity criterion

18 )

Sidesoftwo similar triangles are in the ratio 4:9. Area of these triangles are in the ratio

(a)
2:3
(b)
4:9
(c)
81:16
(d)
16:81

Solution :

Ratio of areas = \(\left(4\over 9 \right)^2=16:81\)

19 )

ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is

(a)
2:1
(b)
1:2
(c)
4:1
(d)
1:4

Solution :

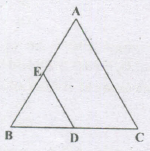
∴ ΔABC and ~ BDE are equilateral
∴ They are similar
\(∴ {ar(ΔABC)\over ar(ΔBDE)}=\left(AB\over BD \right)^2=4:1\)

20 )

In the given figure, AB = 3.4 em;BD = 4 cm,BC = 10 em. Then the value of AC is.

(a)
5.1cm
(b)
3.4cm
(c)
6cm
(d)
5.3cm

Solution :

∴ AD bisects \(\lfloor A\)
∴ \({AB\over AC}={BD\over DC}\)

\(⇒ {3.4\over AC}={4\over 6}⇒AC=5.1cm\)

21 )

The area of two similar triangles is 25 em" and 36 cm²If the median of the smaller rriangle is 10cm. then the median of the larger triangle is

(a)
12 cm
(b)
15 cm
(c)
10 cm
(d)
18 cm

Solution :

∴ The ratio of the area of two similar triangles is equal to the square of the ratio of their corresponding medians
\(∴{ar (smaller\ triangle)\over ar (larger\ triangle)}\)
\(=\left(median\ of\ smaller\ triangle\over median\ of\ larger\ triangle \right)^2\)
\(⇒{25\over 36}=\left(10\over median\ of\ larger\ trianlge \right)^2\)
⇒ median of larger triangle = 12 cm

22 )

In a trapezium ABeD, AB || CD and its diagonal intersect at O. If AB= 6 cm and DC =3 em, then find the ratio of the areas of ΔAOB and ΔCOD

(a)
4:1
(b)
1:2
(c)
2:1
(d)
1:4

Solution :

ΔOAB ~ ΔOCD (MA criterion similarity)
\(∴{ar(ΔOAB)\over ar(ΔOCD)}=\left( AB\over CD\right)^2=\left( 6\over3\right)^2=4:1\)

23 )

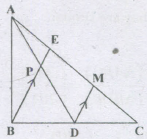
In figure, ΔABC, AD is a median of ΔABC. P is the mid-point of AD.Then ratio of AE and AC is

(a)
1:1
(b)
1:2
(c)
1:3
(d)
2:3

Solution :

In ΔCBE,
∵ D is the midpoint of BC and DM || BE
∴ M is the midpoint of EC
(By BasicProportionality Theorem)
∴ CM = ME ➝ (1)
In ΔADM,
∵ P is the midpoint of AD and PE || DM
∴ E is the midpoint of AM (By BPT)
∴ AE = EM ➝ (2)
From(1) and (2)AE=EM=CM
∴ \(AE={1\over 3}AC\)

24 )

The sides of a triangle are 6 cm, 8 cm and 10 cm. The largest angle of the triangle is

(a)
Acute angle
(b)
Right angle
(c)
Obtuse angle
(d)
Reflex angle

Solution :

∴ 6² + 8² = 10²
∴ By converse of Pythagoras Theorem
The angle between side of length 6 am and 8 cm = 90° which is the largest angle and a right angle,

25 )

If the sides of a triangle are 6 cm, 8 cm and 12 cm, then the nature of the triangle will be

(a)
Right angled
(b)
Obtuse angle
(c)
Acute angled
(d)
Not possible

Solution :

Let AB=6 cm, BC=8 cm and CA=12 cm. Then
CN² > AB² + BC²
\(∴\lfloor C\) is obtuse
∴ ΔABC is obtuse angled.

26 )

The length of the diagonal of as square is 7√2 cm. Then, the area of the square in cm² is

(a)
28
(b)
14√2
(c)
21
(d)
49

Solution :

\(Side ={diagonal\over \sqrt2}=7cm\)
∴ area = 7 x 7 = 49 cm²

27 )

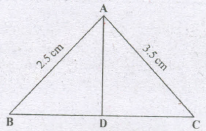
In the figure, the sides AB and AC of ΔABC are 2.5 cm and 3.5 em respectively. IfADis the bisector of ΔBAC, find BD :DC

(a)
4:5
(b)
7:5
(c)
6:7
(d)
5:7

Solution :

∴ AD bisects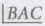
\(∴ {AB\over AC}={BD\over DC}⇒{2.5\over 3.5}={BD\over DC}\)
\(⇒{5\over 7}={BD\over DC}\)

28 )

ΔABC is an isosceles triangle in which \(\lfloor C=90^0\) BC=4 cm. Find AB.

(a)
4√2 cm
(b)
2√2 cm
(c)
4cm
(d)
2cm

Solution :

AC = BC = 4cm

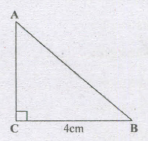
∴ AB²= AC²+BC² (By Pythagoras Theorem)
=4²+4²
⇒ AB = 4√2 cm

29 )

In a \(\triangle ABC,\)

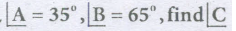
(a)
70^o
(b)
60^o
(c)
80^o
(d)
none of these

Solution :

We know, sum of angles of a triangle is 180^o

30 )

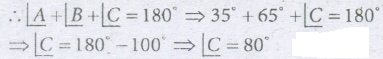
Find the angles of a triangle which are in the ratio 3:4:5

(a)
35^o,45^o,55^o
(b)
45^o,60^o,75^o
(c)
65^o,75^o,85^o
(d)
none of these

Solution :

Let the measure of given angles be (3x)^o,(4x)^o,(5x)^o
3x+4x+5x=180 [\(\therefore\) sum of the angle of a triangle =180^o]
x=15
so, the anges mesaures (3x15)^o,(4x15)^o,(5x15)^o = 45^o,60^o,75^o